2 esquemas volumenes_finitos

1

HIDRÁULICA COMPUTACIONAL 2Máster en Ingeniería del Agua

Introducción al método de

volúmenes finitos

Asignatura: Hidráulica Computacional 2

Profesor: Luis Cea

Luis Cea GómezGrupo de Ingeniería del Agua y del Medio Ambiente, GEAMAUniversidad de A Coruña

2

1. Introducción

2. Mallas de cálculo

3. El método de volúmenes finitos

3.1. La ecuación de convección-difusión

3.2. Propiedades de los esquemas numéricos

3.3. Esquemas centrados

INTRODUCCIÓN AL MÉTODO DE VOLÚMENES FINITOS


Profesor: Luis Cea


3.4. Esquemas descentrados

4. Esquemas en volúmenes finitos para las 2D-SWE

3

� Volúmenes finitos� Impone conservación de forma natural� Flexibilidad geométrica� Resuelve ecuaciones en forma integral (ondas choque)� Discretización muy intuitiva (leyes físicas)

� Elementos finitos� Flexibilidad geométrica� Muy versátil (diferentes áreas de aplicación)

� Diferencias finitasMétodos numéricos

Introducción al método de volúmenes finitos

Introducción


Profesor: Luis Cea

� Diferencias finitas� Discretización sencilla� Problemático en geometrías complicadas

� Smoothed Particle Hydrodynamics� Adecuado para superficie libre compleja� Método sin malla. Lagrangiano� Coste computacional muy elevado� Todavía en desarrollo� Tendencia a creerse los resultados

� Otros

numéricos en CFD

4

Volúmenes finitos


Introducción


Profesor: Luis Cea

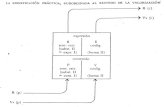
0A)u (ρA)u (ρA)u (ρA)u (ρ snwe =−+−

� Flujo a través de las aristas de las celdas

� Lo que sale de una celda entra en la celda de al lado

� Conservación de masa / momento

5

Volúmenes finitos


Introducción


Profesor: Luis Cea

6

Diferencias finitas

∆y 2

vv

x∆ 2

uu

yv

xu

0 1ji,1ji,j1,ij1,i −+++ −+

−≈

∂∂+

∂∂=


Introducción


Profesor: Luis Cea

Elementos finitos

( ) 0F =φ

( ) ( ) )(C incógnitas-nxfCx~j

n

1jjj∑

=

=φ

ecuaciones-n(0dV )~F(w n)1,iV

i ==⋅∫ φ

7

Smoothed Particle Hydrodynamics


Introducción


Profesor: Luis Cea

8

Smoothed Particle Hydrodynamics


Introducción


Profesor: Luis Cea

9

1. Introducción








Profesor: Luis Cea




10

Malla estructurada vs. Malla no estructurada


Mallas de cálculo


Profesor: Luis Cea

11


Tipos de mallasMalla estructurada cartesiana Malla estructurada por bloques cartesiana

Malla estructurada curvilínea Malla estructurada por bloques

Mallas de cálculo


Profesor: Luis Cea

Malla no-estructurada cartesiana Malla no-estructurada triangular

12

Tamaño de malla

Aspecto fundamental en CFD al que muchas veces no se le presta la atención merecida

Malla más fina en:� contornos pared� recirculaciones� discontinuidades

Ventaja para mallas no estructuradas

Multigrid methods


Mallas de cálculo


Profesor: Luis Cea

13

Convergencia en malla

Malla 1


Mallas de cálculo


Profesor: Luis Cea

14

Tamaño de malla


Mallas de cálculo


Malla 2


Profesor: Luis Cea

15


Mallas de cálculo


Malla 3


Profesor: Luis Cea

16


Mallas de cálculo



Profesor: Luis Cea

17

1. Introducción








Profesor: Luis Cea




18

� Consistente� si tiende a la ecuación diferencial cuando ∆x � 0

� Conservativo � si conserva la masa, el momento, etc. en ausecia de términos fuente

� Transportividad (transportivity ) � si tiene en cuenta la dirección en la que se transmite la información

� Acotado (boundedness)

Propiedades de los esquemas numéricos


Volúmenes finitos


Profesor: Luis Cea

� Acotado (boundedness) � sin términos fuente no se generan máximos ni mínimos locales

� Estabilidad � si no es generan oscilaciones numéricas a partir de errores infinitesimales

� Orden de precisión

Boundedness

para un esquema lineal (ai no depende de U)

Boundedness � aj positivos, ai>= sumatorio aj ∑ −=≤+=

≥

iji

iiii

j

saa

ssbS

a

0

0

φ

19

Sxxx

u

t jjj

j +

∂∂Γ

∂∂=

∂∂

+∂∂ φφφ

La ecuación de convección-difusión 3D

( ) ( ) ∫∫∫ +∇Γ⋅∇=⋅⋅∇+−+

iii VVVi

ni

1ni dV SdV dVV∆t

φφφφu

n1n −+ φφ


Volúmenes finitos


Profesor: Luis Cea

( ) ( )( ) iii

ni

1ni VS V∆t

+⋅∇Γ=⋅⋅+−

∑∑∈∈

+

ii Kjij

Kjij nnu φφφφ

20

ii1/2i1/2ii

ni

1ni ∆xSFFx∆t

=−+∆−−+

+ φφ

∂φ

Sxxx

ut

+

∂∂Γ

∂∂=

∂∂+

∂∂ φφφ


Volúmenes finitos

La ecuación de convección-difusión 1D


Profesor: Luis Cea

( )1/2i

1/2i 1/2i xΓu F

+++

∂∂−= φφ

i

i1i1/2i

1/2i ∆xxΓ

φφφ −Γ=

∂∂ +

++

Convección Difusión

21

Esquema centrado de orden 2

( )22

uuuu 1ii1ii

1/2i1/2i1/2i++

+++++

==φφφφ

∆x

2

2ux

∆t1ii1i1i1i

ni

1ni −+−+

+ +−Γ=

−+∆

− φφφφφφφ

Independiente de Φ


Volúmenes finitos


Profesor: Luis Cea

� Esquema numéricamente inestable

� Permite oscilaciones de Φ en la solución

Independiente de Φi

22

Esquema descentrado de orden 1

0u si

0u si

1/2i1i1/2i

1/2ii1/2i

<=

>=

+++

++

φφφφ

( ) ( )1ii1i21ii

ni

1ni 2

∆x

Γ

∆xu

∆t −+−

+

+−+

−+− φφφφφφφ

( )0cteu >=


Volúmenes finitos


Profesor: Luis Cea

� Esquema numéricamente estable

� No genera oscilaciones de Φ en la solución

� Muy difusivo

( )( )

( )1ii1i21i1ini

1ni 2

∆x

∆t Γ

∆x 2

∆tu

∆x 2

∆tu −+−+

+ +−

++−−= φφφφφφφ

Difusión numéricaDiscretización centrada de orden 2 2

∆xu n =Γ

23

� Hybrid upwind scheme

� Power-law scheme

� QUICK

Otros esquemas


Volúmenes finitos


Profesor: Luis Cea

24

0∆x

FF∆t

ww 1/2i1/2ini

1ni =−+− −+

+

( ) ( )i1i1ii1/2i ww∆t 2∆x

FF21

F −−+= +++ ( )n1i

n1i

ni ww

21

w +− +=

Esquema de Lax-Friedrichs (muy difusivo)

wF

A∂∂=

equivalente a centrado con:

� Condicionalmente estable (CFL<1)

Otros esquemas


Volúmenes finitos


Profesor: Luis Cea

0Asi FF

0AsiFF

1/2i1i1/2i

1/2ii1/2i

<=>=

+++

++

Esquema descentrado de Godunov

� Monótono (CFL<1)

( ) ( )i1i1/2i1ii1/2i wwA21

FF21

F −−+= ++++

25

0∆x

FF∆t

ww 1/2i1/2ini

1ni =−+− −+

+

wF

A∂∂=

Esquema de Lax-Wendroff de 2 pasos

� Condicionalmente estable (CFL<1)

Otros esquemas


Volúmenes finitos

)F(wF)F(F∆x∆t

21

)w(w21

w LW21/2i1/2ii1i

n1i

ni

LW21/2i +++++ =→−−+=


Profesor: Luis Cea

� No monótono

Esquema centrado de Godunov

)F(wF)F(F∆x∆t

)w(w21

w GC1/2i1/2i

ni

n1i

n1i

ni

GC1/2i +++++ =→−−+=

� Condicionalmente estable (CFL < 0.707)� Monótono para 0.5 < CFL < 0.707� Oscilatorio para CFL < 0.5

26

Otros esquemas

Esquema FORCE

−−+= +++

∆x1

)F(F∆x∆t

21

)w(w21

w i1in

1ini

LW21/2i


Volúmenes finitos

0∆x

FF∆t

ww 1/2i1/2ini

1ni =−+− −+

+

wF

A∂∂=


Profesor: Luis Cea

−−++= ++++ )w(w∆t∆x

F)2F(wF41

F ni

n1i1i

LW21/2ii

force1/2i

� Condicionalmente estable (CFL<1)� Monótono (CFL<1)

27

0x

F(w)tw =

∂∂+

∂∂

[ ]1/2i1/2ini

1ni FF

∆x∆t

ww −++ −−=

Métodos conservativos


Volúmenes finitos


Profesor: Luis Cea

Fi+1/2 Flujo a través de las aristas de las celdas

Lo que sale de una celda entra en la celda de al lado

Conservación de masa / momento

28

0xq

th =

∂∂+

∂∂

Ejemplo: Conservación de masa 1D

0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

uhq ⋅=


Volúmenes finitos


Profesor: Luis Cea

? q ¿ 1/2i+

29

Ejemplo: Conservación de masa 1D


Volúmenes finitos

0xq

th =

∂∂+

∂∂

0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

uhq ⋅=


Profesor: Luis Cea

+

+

++

=+

++

++

+

otras

h2uu2

uhuh2uu

2hh

q

i1ii

1i1iii

1ii1ii

1/2i

Centrado

Centrado

Descentrado

30

0∆x 2

uhuh∆t

hh 1i1i1i1ini

1ni =−+− −−++

+

Ejemplo: Esquema centrado 1D

� Esquema numéricamente inestable

� Permite oscilaciones de h en la solución

Independiente de hi


Volúmenes finitos


Profesor: Luis Cea

1n1i

n1i

1n1i

n1i

ni

1ni hu

∆x 2∆t

hu∆x 2∆t

hh +++

+−−

+ −+=

Coef. negativo � esquema NO monótono� puede generar oscilaciones (inestabilidades)

31

Ejemplo: Esquema descentrado 1D

0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

0xq

th =

∂∂+

∂∂


Volúmenes finitos


Profesor: Luis Cea

32


0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

>

= + 0usiqq 1/2ii

0xq

th =

∂∂+

∂∂


Volúmenes finitos


Profesor: Luis Cea

<

=++

++ 0usiq

q1/2i1i

1/2ii1/2i

33


0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

>

= + 0usiqq 1/2ii

0xq

th =

∂∂+

∂∂

0qqhh 1ii

ni

1ni =−+− −

+


Volúmenes finitos


Profesor: Luis Cea

<

=++

++ 0usiq

q1/2i1i

1/2ii1/2i 0

∆xqq

∆thh 1iiii =−+− −

34


0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

>

= + 0usiqq 1/2ii

0xq

th =

∂∂+

∂∂

0qqhh 1ii

ni

1ni =−+− −

+


Volúmenes finitos


Profesor: Luis Cea

<

=++

++ 0usiq

q1/2i1i

1/2ii1/2i 0

∆xqq


( )21ii1i1i1i

ni

1ni

∆x

q2qq2∆x

x 2qq

∆thh −+−+

+ +−=∆−+−

35


0∆x

qq∆t

hh 1/2i1/2ini

1ni =−+− −+

+

>

= + 0usiqq 1/2ii

0xq

th =

∂∂+

∂∂

0qqhh 1ii

ni

1ni =−+− −

+


Volúmenes finitos


Profesor: Luis Cea

<

=++

++ 0usiq

q1/2i1i

1/2ii1/2i 0

∆xqq


( )21ii1i1i1i

ni

1ni

∆x

q2qq2∆x

x 2qq

∆thh −+−+

+ +−=∆−+−

2

2

xq

2∆x

xq

th

∂∂=

∂∂+

∂∂

Difusión numérica

36

0∆x

qq∆t

hh n1i

ni

ni

1ni =−+− −

+


0∆x

qq∆t

hh 1n1i

1ni

ni

1ni =−+− +

−++

n1i

n1i

ni

ni

1ni hu

∆x∆t

u∆x∆t

1hh −−+ +

−= 1n1i

n1i

ni

ni

1ni hu

∆x∆t

hu∆x∆t

1h +−−

+ +=

+⋅

Discretización Explicita Discretización Implicita


Volúmenes finitos


Profesor: Luis Cea

1i1iiii hu∆x

u∆x

1hh −−+

−=1i1iiii hu

∆xhu

∆x1h −−+=

+⋅

ni

ni

ni u

∆x∆t1u

∆x∆t

CFL0u∆x∆t

1 <→<=→>− Restricción sobre el paso de integración temporal

Condición CFLCourant-Friedrichs-Levy

Esquema monótono (estable)Coeficientes positivos

37

Esquemas descentrados de Godunov

[ ]1/2i1/2ini

1ni FF

∆x∆t

ww −++ −−=

0))(x/tF(wF 1/2i1/2i == ++ Flujo numérico

0x

F(w)tw =

∂∂+

∂∂


Volúmenes finitos


Profesor: Luis Cea

0))(x/tF(wF 1/2i1/2i == ++ Flujo numérico

(x/t)w 1/2i+ solución del problema de Riemann

><

=

=∂+∂

+ 0x ifw

0x ifww(x,0)

0F(w)w

n1i

ni

xt

38

Esquemas descentrados de Godunov

Riemann Solvers

(0))F(wF 1/2i1/2i ++ = aproximado(x/t)w 1/2i+

� Primera opción resolver el problema de Riemann de forma exacta (no analítico)

� Resolventes de Riemann aproximadas (approximate Riemann solvers )

� Aproximar el estado de Riemann


Volúmenes finitos


Profesor: Luis Cea

1/2iF+ aproximar el flujo directamente

� Aproximar el flujo de Riemann

Roe Esquema de Roe

HLL Harten - Lax - van Leer (mucha difusión en discontinuidades de contacto, vórtices)

HLLC Harten - Lax - van Leer Contact

( ) ( )i1i1/2i1ii1/2i wwA21

FF21

F −−+= ++++

39

1. Introducción








Profesor: Luis Cea




40

∑=∂∂

+∂∂+

∂∂

kk

yx Gy

F

xF

tw

Ecuaciones de aguas someras en forma vectorial y conservativa

=

+=

=h

qq

q

F2

gh

h

q

q

Fq

h

w yx

y

y

22x

x

xx

∂∂

∂∂−=

−−=

∂∂

∂=j

je

j3xb,2

b1 x

Uhν

x

0

G

τ

τ

0

GxZ

gh-

0

G

� Sistema de 3 ecuaciones con 3 incógnitas

� Definido en un dominio 2D


Esquemas numéricos para 2D-SWE


Profesor: Luis Cea

( ) i

3

1kik,L yyxxi

ni

1ni AGdLn~Fn~FA∆t

wwi

∑∫=

+

=++−

Flujo convectivo Término fuente

Discretización temporal y espacial

+

2

gh

h

qh

h

qq2h

q22

yyxy

∂∂

∂∂−

∂∂

−

∂∂∂

j

je

j

jjyb,b

x

Uhν

x

xxτ

yZ

gh-

x

41

( ) ∑∫∈

≈+i

i KjijRLijL yyxx )n,w,(wFdLn~Fn~F

Flujo numérico

Esquemas descentrados de GodunovFlujo convectivo




Profesor: Luis Cea

Estado medio de cada celda

Flujo normal entre celdas

Fij Proyección 1D del flujo normal entre celdas

42

( ) ∑∫∈

≈+i

i KjijRLijL yyxx )n,w,(wFdLn~Fn~F

Flujo numérico

( ) yyxxLRLRRL

ij nFnFZwwA21

2ZZ

F +=−−+=

Esquemas descentrados de GodunovFlujo convectivo




Profesor: Luis Cea

LR22

Centrado Upwind Flujo normal

Matriz |A| de descentramiento� Roe (1986) con regularización de Harten (1983)

� HLL. Harten – Lax – van Leer

� HLLC . Harten – Lax – van Leer - Contact

43

Extensión a orden 2

Esquemas tipo WAFWeight Averaged Flux

Esquemas tipo MUSCLMonotone Upstram Scheme for Conservative Laws




Profesor: Luis Cea

44

[ ]waf1/2-i

waf1/2i

ni

1ni FF

∆x∆t

ww −−= ++ x∆1β x∆2β

λ=tx /

2

t∆

t∆

A B C• ••

Extensión a orden 2 Esquemas tipo WAF




Profesor: Luis Cea

t

0

niq

niq

n1iq +

n1iq +

1/2ix + 2

x∆−2

x∆

)(A wc)(121

)(A wc)(121

F n1i

ni

waf1/2i ++ ⋅−+⋅+=

WAF ~ Lax-Wendroff si c<1

45

1. Se realiza una reconstrucción lineal de las variables en cada celda a partir del valor medio en la celda y del gradiente

Extensión a orden 2 Esquemas tipo MUSCL




Profesor: Luis Cea

2. Extrapolación lineal de las variables conservadas de los nodos a las aristas

3. Los valores extrapolados se utilizan en vez de los valores nodales en el esquema de Godunov correspondiente (Roe, van Leer, HLL, ...)

( ) ∑∫∈

≈+i

i KjijiJIjijL yyxx )n,w,(wFdL n~Fn~F

46


Orden 2 . Oscilaciones espúrias




Profesor: Luis Cea

Esquemas de alta resolución� Orden 2 excepto en discontinuidades� Sin oscilaciones espúrias � Alta resolución en discontinuidades

47


Lax-Wendroff Godunov-Upwind




Profesor: Luis Cea

48

)w,...,w,...,H(ww nri

ni

nsi

1ni +−

+ =

j todopara 0wH

nj

≥∂∂

Esquema monótono

∑=+

j

njj

1ni waw

Esquema monótono

lineal no Esquema(w)aa

lineal Esquemactea

jj

j

→=

→=




Profesor: Luis Cea

j

j todopara 0aj ≥Esquema lineal monótono

Teorema de GodunovEsquemas lineales monótonos son de primer orden

( ) ( )( ) ( )n

i1n

i

ni

1ni

1ni

1ni

ni

ni

qminqmin

qmaxqmax

i qwi qw

≥

≤

∀≥→∀≥

+

+

++

Esquema monótono

49

Extensión a orden 2 Esquemas de alta resolución TVD

Propiedad TVDTotal Variation Diminishing

)TV(u )TV(uTVD

uu)TV(u

n1n

i

ni

n1i

n

<→

−=

+

+∑




Profesor: Luis Cea

� No se generan extremos locales� Los máximos locales no aumentan� Los mínimos locales no disminuyen

Teorema de HartenEsquema Monótono � Esquema TVD (condición suficiente, no necesaria)

Coeficientes Positivos � TVD (condición suficiente pero no necesaria )

50

Extensión a orden 2 Esquemas de alta resolución TVD tipo MUSCL

)w(wα ww ijiIj −⋅≤−

0)ww()w(w ijiIj >−⋅−

Limitadores de pendiente

Se imponen 2 condiciones:




Profesor: Luis Cea

0)ww()w(w ijiIj >−⋅−

( )[ ]( )[ ])w(wα),w-(wmax 0,min∆0)w(w

)w(wα),w-(wmin 0,max∆0)w(w

ijiIj*iij

ijiIj*iij

−⋅=→<−

−⋅=→>−

MinmodLimitador 0.5α

SuperbeeLimitador 1α

→=→=

51

i

b22

xz

ghgh21

hUxt

hU∂∂−=

+∂∂+

∂∂ ( )

ii

b2

xh

ghxz

ghhUxt

hU∂∂−

∂∂−=

∂∂+

∂∂

� Equivalentes en flujo gradualmente variado

Formulación A Formulación B

xF xF




Profesor: Luis Cea

� Diferentes en ondas de choque, resaltos hidráulicos

� Formulación A más precisa si hay choques / cambios de régimen

� Formulación B más sencilla / menos problemas con términos fuente

Preferible formulación A

52

i

b22

xz

ghgh21

hUxt

hU∂∂−=

+∂∂+

∂∂

Formulación A

Condiciones hidrostáticas

bzgh

hgh

∂−=∂




Profesor: Luis Cea

Discretización descentrada de términos fuente

i

b

xgh

xgh

∂−=

∂

Descentrado Centrado

Errores en el equilibrio si fondo irregular

53

Discretización descentrada del flujo convectivo:� estabiliza el esquema, pero� introduce difusión numerica en las ecuaciones

Discretización descentrada de términos fuenteVázquez-Cendón (1994), Bermúdez et al. (1998)

Ld� Discretización descentrada para términos fuente en general




Profesor: Luis Cea

∑∈

−≈iKj

ij1-ijij

ijij

i

Cii S

~QQ

2

Ld

A

1SS

� Correcciones de orden 2 para pendiente del fondo

iIKj

ijij

ii

*i S

~

2

Ld

A

1SS

i

∑∈

−≈

54

Término fricción fondo

A. Discretización explicita

qqCxz

ghgh21

hUxt

hUf

i

b22 ⋅−∂∂−=

+∂∂+

∂∂

qq CIh gρ

τf

b ⋅==7/3

2

f hn g

C =




Profesor: Luis Cea

n

i

ni

nif,

ni

ni

ni

1ni qq CSC∆t

qq ⋅−=+−+

Inestabilidades si fricción importante, valores negativos

( ) ( )ni

ni

n

i

nif,

ni

1ni SC∆tq C1qq +−⋅+−⋅=+

55

Término fricción fondo

B. Discretización semi-implicita

qqCxz

ghgh21

hUxt

hUf

i

b22 ⋅−∂∂−=

+∂∂+

∂∂

qq CIh gρ

τf

b ⋅==7/3

2

f hn g

C =




Profesor: Luis Cea

n

i

1ni

nif,

ni

ni

ni

1ni q q CSC∆t

qq ++

−=+−

( ) ( )ni

ni

ni

n

i

nif,

1ni SC∆tqqC∆t1q +−⋅+=⋅⋅++

Siempre positivo �� no genera Inestabilidades

56

Término difusivo (laminar / turbulento)

A. Discretización explicita




Profesor: Luis Cea

B. Discretización semi-implicita||tot DDD += ⊥

( )ix,jx,D UUΓD −=⊥⊥

( )Vx,Bx,D|| UUΓD||

−=

57

Contornos tipo pared




Profesor: Luis Cea

Condición de deslizamiento libre

0y

ε0

y

k

0τ0V

ww

ww

=∂∂=

∂∂

==

Condición de no deslizamiento

2

2

ww

ww

y

kνε0k

0V0U

∂∂==

==

malla de pared muy fina

1y ≈+malla de pared gruesa

100y >>+

58

� Discretización del fondo en escalones de altura constante

� Parametro εwd para definir el frente seco-mojado

� Redefinición del fondo� Condición de reflexión en el frente qn=0

Tratamiento del frente seco-mojado

jb,i Zwse <




Profesor: Luis Cea

� Condición de reflexión en el frente qn=0� Flujos normales = 0 en el frente

� No se redefine el fondo � No se aplica condición de reflexión

jb,i Zwse >

2 esquemas volumenes_finitos

Education

Transcript of 2 esquemas volumenes_finitos