Integrales Indefinidas-Iniciación
-
Upload
nublado123 -
Category
Documents
-
view
5 -
download
0
description
Transcript of Integrales Indefinidas-Iniciación

INTEGRÁLES INDEFINIDAS.
1. PRIMITIVA E INTEGRAL INDEFINIDA DE UNA FUNCIÓN.
EJEMPLO:
Sea la función: f(x) = x2
“Una Primitiva de f” es otra función F, tal que, la derivada de F es f, es decir:
F’(x) = f(x)
Con la función anterior, ¿qué habría que poner dentro del recuadro?:
‘ = x2
Se puede comprobar que como función F vale: x3/3
También puede comprobarse que vale como primitiva: F(x) = x3/3 + 5
En general, vale como Primitiva de f(x) = x2 : F(x) = x3/3 + C, siendo C una cte.
Al conjunto de TODAS las primitivas de una función f se le llama “ INTEGRAL INDEFINIDA DE f “ y se representa por f(x)dx, que se lee “Integral de f de x diferencial de x”
El signo de la operación de integración es una letra “ese” alargada. “Ese” de suma, pues las integrales indefinidas se usan principalmente para hallar la suma de infinitas funciones infinitesimales ó “INTEGRAL DEFINIDA”.
Luego:
, siendo F(x) una primitiva cualquiera y C una cte llamada “cte de integración”
En el ejemplo anterior, escribiríamos: x2dx = x3/3 + C
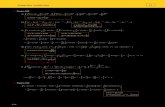
2. TABLA DE LAS INTEGRALES “INMEDIATAS”.
Se pueden comprobar fácilmente:
f(x)dx = F(x) + C
1

1ª) Integral Inmediata: 0dx = C siendo 0 = función nula
2ª) kdx = kx + C
EJEMPLOS:
1) 5dx = 5x + C
2) dx = 1dx = 1·x + C
3ª) Si a -1, [f(x)]·f’(x)dx =
EJEMPLOS:
1) (x2+1)32xdx
Para resolverla:
1º) ¿Cuánto vale la potencia?
2º) ¿Quien es a, f y f’?
3º) Completar f’. Para ello:
Multiplicar ó dividir por el número que falte y procediendo en sentido contrario delante de la integral.
ó Sacar fuera de la integral las ctes que sobren
f’ HACE FALTA PERO DESPUÉS NO SE PONE EN EL RESULTADO.
2) sen3x · cos x dx
3)
4)
5) sen x · cos x dx
2

4ª) Es el tercer tipo cuando a = -1
EJEMPLOS:
1)
2)
5ª)
EJEMPLO:
6ª) af(x)· f’(x)dx =
EJEMPLO:
2sen x·cosxdxCASO PARTICULAR IMPORTANTE:
ef(x)·f’(x)dx = ef(x) + C
EJEMPLOS:
1) esen x · cos xdx
2)
7ª) [cos f(x)]·f’(x)dx = sen f(x) + C
3

8ª) [sen f(x)]·f’(x)dx = -cos f(x) + C
9ª) = tg[f(x)] + C
10ª) = -cotg[f(x)] + C
11ª) = arcsen[f(x)] + C
12ª) Integral Inmediata: = arctg[f(x)] + C
3ª PREGUNTA: PROPIEDADES DE LAS INTEGRALES INDEFINIDAS.
1ª) Propiedad: (f(x) g(x)) dx = f(x)dx g(x)dx
EN ESTA PROPIEDAD SE BASA LA TÉCNICA DE INTEGRACIÓN “ POR DESCOMPOSICIÓN DEL INTEGRANDO”
EJEMPLOS:
1) (x3+x2+7)dx
2) (sen x - )dx
3ª) Propiedad: kf(x)dx = k f(x)dx
4

EN ESTA PROPIEDAD SE BASA LA TÉCNICA DE INTEGRACIÓN : “ REDUCIBLES A INMEDIATA”
EJEMPLO:
3x4dx
3ª) Propiedad: f(x) · g(x) dx f(x)dx · g(x)dx
4ª PREGUNTA : MÉTODOS Ó TÉCNICAS DE INTEGRACIÓN.
En este Curso veremos SÓLAMENTE DOS Técnicas de Integración:
1ª) Integrales reducibles a inmediatas. Se basan en la propiedad:
kf(x)dx = k f(x)dx
2ª) Integración por descomposición del Integrando. Se basan en la propiedad:
(f(x) g(x)) dx = f(x)dx g(x)dx
5ª PREGUNTA: INTEGRALES REDUCIBLES A INMEDIATAS.
PRIMER TIPO: Integrales reducibles a una del tipo:
Si a -1, [f(x)]·f’(x)dx =
EJERCICIOS:
1)
Para resolverla:
1º) ¿Cuánto vale la potencia?
2º) ¿Quien es a, f y f’?
3º) Completar f’. Para ello:
5

Multiplicar ó dividir por el número que falte y procediendo en sentido contrario delante de la integral.
ó Sacar fuera de la integral las ctes que sobren
f’ HACE FALTA PERO DESPUÉS NO SE PONE EN EL RESULTADO.
2) x-1/3dx
3) (x+1)2dx
4) dx
5) x2·(2-x3)3dx
6)
7)
8) sen 2x · cos 2x dx
9)
10)
11)
6

SEGUNDO TIPO: Integrales reducibles a una del tipo:
EJERCICIOS:
1)
2)
3) sen x · cos-1 x dx
4)
5)
6)
7)
8) tg xdx
7

TERCER TIPO: Integrales reducibles a una del tipo:
af(x)· f’(x)dx =
EJERCICIOS:
1) e-xdx
2) 4e2xdx
3) sen x · ecos x dx
4) 2ex/3dx
5)
CUARTO TIPO: Integrales reducibles a una del tipo:
[cosf(x)]·f’(x)dx = sen f(x) + C
EJERCICIOS:
1) cos(2x+1)dx
2) x·cos(x2+5) dx
3) (5x4+3)·cos (x5+3x+4)dx
4)
8

5) excos exdx
QUINTO TIPO: Integrales reducibles a una del tipo:
[sen f(x)]·f’(x)dx = -cos f(x) + C
EJERCICIOS:
1) sen (7x+8)dx
2)
3) (x-3)·sen (x2-6x+1)dx
4)
SEXTO TIPO: Integrales reducibles a una del tipo:
= tg[f(x)] + C
EJERCICIOS:
1)
2)
3)
9

4)
SÉPTIMO TIPO: Integrales reducibles a una del tipo:
= -cotg[f(x)] + C
EJERCICIOS:
1)
2)
3)
OCTAVO TIPO: Integrales reducibles a una del tipo:
= arcsen[f(x)] + C
EJERCICIOS:
1)
2)
3)
4)
10

5)
NOVENO TIPO: Integrales reducibles a una del tipo:
= arctg[f(x)] + C
EJERCICIOS:
1)
2)
3)
4)
5)
6)
7)
6ª PREGUNTA: INTEGRACIÓN POR DESCOMPOSICIÓN DEL INTEGRANDO.
11

a) Aparece la integral de una función potencial.
Haremos uso de la propiedad:
EJERCICIOS:
1)
2)
b) Resulta un logaritmo neperiano más un arcotangente.
EJERCICIOS:
1)
2)
3)
EJERCICIOS DE REPASO DE LO MÁS DIFICIL.
1) Integrales de funciones potenciales:
a) ( hay que obtener una sola x elevada a un número, pues x’ = 1)
b)
12

c)
2) Poner ejercicios parecidos a los que hay en las preguntas 5ª) y 6ª), que tienen asteriscos y que dan por resultado:
a) Arcoseno
b) Arcotangente
c) Logaritmo neperiano más un arcotangente. ( SÓLO ESTOS TIPOS SE REPASARÁN )
13