INTRODUCCION A LAS ONDAS

15 de diciembre de 2009

Indice general

1. Ondas en una dimension. 3

1.1. Definicion, ecuacion general y algunas propiedades generales. . . . . . . . . . . . . . . . . . . . . 41.2. Ondas periodicas y ondas armonicas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51.3. Expresion compleja de las ondas armonicas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2. Ondas transversales en una cuerda. 7

2.1. Ecuacion de ondas en una cuerda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82.2. Densidades de energıa cinetica, potencial, energıa mecanica y potencia transmitida por la onda

en un punto de una cuerda y en un instante dado . . . . . . . . . . . . . . . . . . . . . . . . . . . 92.3. Ondas estacionarias en una cuerda de longitud finita . . . . . . . . . . . . . . . . . . . . . . . . . 9

2.3.1. Nodos y vientres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102.3.2. Energıa cinetica, potencial, mecanica en una onda y potencia transmitida por un punto

en el caso de una onda estacionaria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112.4. Ondas armonicas que se propagan en una cuerda . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

2.4.1. Energıa cinetica, potencial y mecanica en una onda que se propaga . . . . . . . . . . . . . 132.4.2. Potencia transmitida por un punto de una onda que se propaga . . . . . . . . . . . . . . . 13

2.5. Impedancia de una cuerda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142.6. Cambio de medio: reflexion y transmision de ondas en el contorno de una cuerda . . . . . . . . . 14

2.6.1. Coeficientes de transmision y reflexion para la energıa . . . . . . . . . . . . . . . . . . . . 15

3. Ondas longitudinales en gases: ondas sonoras 16

3.1. Ondas longitudinales en un tubo cilındrico lleno de un gas ideal . . . . . . . . . . . . . . . . . . . 173.1.1. Demostracion de la ecuacion de ondas longitudinales en un gas . . . . . . . . . . . . . . . 17

3.2. Ecuaciones de las ondas acusticas para las demas magnitudes del gas . . . . . . . . . . . . . . . . 183.3. Relaciones de fase y amplitud entre las diversas perturbaciones en una onda de presion . . . . . . 193.4. Potencia transportada por una onda sonora. Intensidad y sensacion sonora . . . . . . . . . . . . . 19

3.4.1. Intensidad. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203.4.2. Sensacion sonora, nivel de intensidad sonora . . . . . . . . . . . . . . . . . . . . . . . . . . 20

3.5. Impedancia de una onda acustica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203.6. Densidades de energıa cinetica, potencial y mecanica . . . . . . . . . . . . . . . . . . . . . . . . . 203.7. Ondas esfericas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203.8. Condiciones de contorno en tubos sonoros . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

3.8.1. Coeficientes de transmision y reflexion para la velocidad de oscilacion y la presion . . . . 223.8.2. Coeficientes de transmision y reflexion para la energıa . . . . . . . . . . . . . . . . . . . . 23

A. Apendice 24

A.1. Integracion de funciones trigonometricas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25A.1.1. Formas directas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25A.1.2. Expresiones usadas en ondas estacionarias . . . . . . . . . . . . . . . . . . . . . . . . . . . 25A.1.3. Expresiones usadas en ondas armonicas que se propagan . . . . . . . . . . . . . . . . . . . 26

Capıtulo 1

Ondas en una dimension.

4 Ondas

1.1. Definicion, ecuacion general y algunas propiedades generales.

Definicion: Una onda es una perturbacion local del estado de equilibrio que se propaga en un medio. En

el caso de las ondas electromagneticas, esa perturbacion se puede propagar en el vacio.

De momento se van a considerar solamente ondas que se propagan en una direccion espacial o casos quese pueden reducir a este, p.ej. ondas esfericas.

La funcion real, que describe estas ondas, depende de una sola variable espacial, x, y el tiempo t. Si estafuncion se describe como f(x, t), debe ser solucion de la ecuacion general:

∂2f

∂t2(x, t) = c2

∂2f

∂x2(x, t)

donde c es la velocidad de propagacion de la onda, es decir, la velocidad con que se propaga la perturbacion

en el medio. Tambien se conoce con el nombre de velocidad de fase.

Generalmente, el calculo de la expresion de c es laborioso y acompana a la deduccion de la ecuacion deondas, para el caso concreto que se trate. Un caso particularmente simple para obtener la expresion de ces el de las ondas electromagneticas.

De ahora en adelante toda solucion de una ecuacion de este tipo es una onda.

Principio de superposicion: Las derivadas segundas son operadores lineales. Es decir, la derivada segundade una combinacion lineal, a coeficientes reales y constantes, de solucionnes de la ecuacion de ondases solucion de esta ecuacion. Por tanto, toda combinacion lineal a coeficientes constantes de ondas esuna onda. Ası se explican fenomenos fısicos como la interferencia y difraccion. Ası se explica tambien laposibilidad de descomponer los sonidos en notas y la luz blanca en el arco iris.

Solucion general de la ecuacion de ondas:

Una solucion es f(x, t) = ϕ(x − ct), siendo ϕ una funcion derivable dos veces con continuidad, como essencillo verificar. Ası mismo, f(x, t) = ψ(x+ct), siendo ψ una funcion derivable dos veces con continuidad,tambien es una solucion de la ecuacion de ondas. De acuerdo con el principio de superposicion la soluciongeneral de la ecuacion de ondas en una dimension es:

f(x, t) = ϕ(x− ct) + ψ(x+ ct)

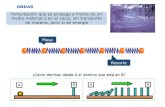
Significado fısico de f(x, t) = ϕ(x − ct) y f(x, t) = ψ(x + ct) . Si se conoce la forma inicial de la onda,f(x, 0) = ϕ(x), y que se propaga hacia la derecha con una velocidad c, la forma de la onda, en el instantet > 0 y en el punto x, es la misma que tenıa inicialmente en el punto x− ct. Es decir se cumple:

f(x, 0) = ϕ(x) =⇒ f(x, t) = f(x− ct, 0) = ϕ(x− ct)

c t

X

x − ct x

t = 0s t > 0sx’ − ct x’

Fig. 1- Onda que se propaga hacia la derecha.

Si se cambia c por −c es trivial ver que la onda ψ(x + ct) se propaga hacia la izquierda.

Ondas 5

1.2. Ondas periodicas y ondas armonicas.

Una onda es periodica en el tiempo y su periodo es T , si en todo punto y en todo instante se verifica:

ϕ(x, t) = ϕ(x, t+ T )

Una onda es periodica espacialmente y su periodo espacial es λ, longitud de onda, si en todo punto y en

todo instante se verifica: ϕ(x, t) = ϕ(x + λ, t)

La longitud de onda y el periodo estan relacionados entre sı.

ϕ(x, t) = ϕ(x+ λ, t) = ϕ(x+ λ− ct) = ϕ(x, t− T ) = ϕ(x − ct+ cT )

⇒ x+ λ− ct = x− ct+ cT =⇒ λ = cT

Se llama frecuencia, ν, a la inversa del periodo. En general sus unidades son las de tiempo a la potenciamenos uno. Cuando el periodo se mide en segundos, la frecuencia se mide en hercios, Hz. Al producto2πν = ω se le denomina frecuencia angular y se mide en rad/s.

Se denomina numero de ondas a k = 2π/λ y se mide en rad/m, cuando λ se mide en m.

Se verifica:

λ = cT ⇒ c = λν =ω

k

Las ondas armonicas son las que se pueden expresar como una funcion sinusoidal. Por ejemplo: ϕ(x, t) =A cos(kx− ωt+ α). La forma de expresar esta onda armonica es equivalente a expresarla como: ϕ(x, t) =A sin(kx− ωt+ β). En efecto:

A cos(kx− ωt+ α) = A sin(kx− ωt+ β) ⇒ cos(kx− ωt+ α) = sin(kx− ωt+ β) ⇒

cos(kx− ωt) cosα− sin(kx− ωt) sinα = cos(kx− ωt) sinβ + sin(kx− ωt) cosα ⇒ sinβ = cosα y

cosβ = − sinα ⇒ β = α+π

2.

Como se puede ver ambas formas son equivalentes.

Las ondas armonicas son siempre periodicas, pero existen ondas periodicas que no son armonicas, p.ej. lasolas.

Una onda que se propaga transporta siempre cantidad de movimiento, momento angular y energıa, pero

nunca materia. En ocasiones las aproximaciones, hechas para obtener la ecuacion de ondas, impidencalcular la cantidad de movimiento transportada por la onda. Es el precio a pagar para tener una ecuacionde ondas de manejo sencillo.

Las ondas pueden ser: transversales, si su velocidad de propagacion es perpendicular a la perturbacion

del medio, y longitudinales, si su velocidad de propagacion y la perturbacion tienen la misma direccion.Las ondas electromagneticas y las ondas transversales en una cuerda son ondas transversales. Las ondassonoras son longitudinales.

1.3. Expresion compleja de las ondas armonicas.

Las ondas armonicas se pueden expresar indistintamente como:

ϕ(x, t) = A cos(kx− ωt+ α) y ϕ(x, t) = A sin(kx− ωt+ β)

Teniendo en cuenta la relacion entre α y β, ambas formas corresponden a la parte real de las exponencialescomplejas: Aei(kx−ωt+α) y Aei(kx−ωt+β).Demostracion:

ℜ

(

Aei(kx−ωt+α))

= ℜ (A cos(kx− ωt+ α) + iA sin(kx− ωt+ α)) = A cos(kx− ωt+ α)

ℜ

(

−iAei(kx−ωt+β))

= ℜ (A sin(kx− ωt+ β) − iA cos(kx− ωt+ β)) = A sin(kx− ωt+ β)

Para calcular, se usa todo el complejo pero al final solo cuenta la parte real como solucion.

6 Ondas

1. Ejemplo: Superposicion de dos ondas de la misma amplitud y fase pero que se propagan en sentidocontrario.

Sean ϕ1(x, t) = Aei(kx−ωt+α) y ϕ2(x, t) = Ae−i(kx+ωt+α), la onda resultante es:

ϕ(x, t) = ℜ

(

Ae−iωt[

ei(kx+α) + e−i(kx+α)])

= 2A cos(kx+ α) sinωt.

La onda resultante es una onda que no se propaga y que, por esta razon se llama onda estacionaria.Mas adelante se varan las ondas estacionarias con mas detalle.

2. Ejemplo: Superposicion de dos ondas de la misma amplitud, cuyas fases difieren en un terminoconstante.

Sean las dos ondas: ϕ1(x, t) = Aei(kx−ωt) y ϕ2(x, t) = Aei(kx−ωt+α). Con α constante y que cumple:0 ≤ α ≤ 2π.

La onda resultante de la superposicion de ambas es:

ϕ(x, t) = ϕ1(x, t) + ϕ2(x, t) = Aei(kx−ωt)(1 + eiα) = Aei(kx−ωt+ α

2)(

e−i α

2 + ei α

2

)

⇒

ϕ(x, t) = 2A cosα

2ei(kx−ωt−α

2) .

Como puede verse la amplitud de la onda depende de α y la fase de ϕ(x, t) es la bisectriz de ambasfases. Cuando α = 0, ϕ(x, t) = 2Aei(kx−ωt y se dice que la superposicion de estas dos ondas es unainterferencia constructiva. Cuando α = π, ϕ(x, t) ≡ 0 y se tiene una interferencia destructiva.

Capıtulo 2

Ondas transversales en una cuerda.

8 Ondas

2.1. Ecuacion de ondas en una cuerda

Se va a considerar una cuerda de densidad de masa constante, µ, pero cuyo peso puede despreciarse frente a lastensiones aplicadas en sus extremos.

1. En principio, su posicion de equilibrio es horizontal y se toma como eje x, la ecuacion de esta posicion esy = 0. El desplazamiento de la posicion de equilibrio es y(x, t) porque depende del punto considerado ydel instante en el que se considera.

2. La perturbacion de la posicion de equilibrio se transmite a lo largo de la cuerda, su velocidad de propagaciones horizontal.

3. Se va a considerar la cuerda muy poco extensible, su longitud se puede considerar constante a primerorden y los deplazamientos de la posicion de equilibrio se pueden considerar verticales. Esta aproximacionhace que el calculo de la cantidad de movimiento, transportada por la onda, de cero como resultado.

4. Todas las deformaciones y sus derivadas seran pequenas, para que la aproximacion sea valida en todopunto y en todo instante. Considerando esta hipotesis, se cumple:

∆l(x, t) = ∆x

√

1 +

(

∂y

∂x

)2

≈ ∆x

Para todo angulo θ se verifica: sin θ ≈ θ ≈ tan θ y cos θ ≈ 1.

T2

T1

α +∆ α

α

x + ∆xx

+ ∆

y

y y

Las ecuaciones de movimiento son:

(µ∆x)x = T2 cos(α+ ∆α) − T1 cosα = 0

µ∆x∂2y

∂t2(x, t) = T2 sin(α + ∆α) − T1 sinα

teniendo en cuenta las relaciones de angulos pequenos, se tiene:

T1 − T2 = 0 ⇒ T1 = T2 = T

∆xµ∂2y

∂t2(x, t) = T sin(α+ ∆α) − T sinα ≈ ∆xT

∂2y

∂x2⇒ µ

∂2y

∂t2(x, t) = T

∂2y

∂x2(x, t)

Dado que T > 0 y µ > 0, existe un cuadrado real c2 =T

µy la ecuacion es:

Ondas 9

∂2y

∂t2(x, t) = c2

∂2y

∂x2(x, t)

la velocidad de propagacion de las ondas transversales en la cuerda es: c =

√

T

µ. Es trivial comprobar que c

tiene las dimensiones de una velocidad. T es una fuerza y µ una densidad lineal de masa. Las dimensiones de c

son: [c] =

(

MLT −2

ML−1

)

1

2

=L

T, que son las dimensiones de la velocidad.

La solucion general sera de la forma: y(x, t) = ϕ(x− ct) + ψ(x+ ct), como se ha visto antes.

Una onda armonica, que se propaga hacia la derecha, es de la forma: y(x, t) = A cos(kx− ωt+ α). Una, que sepropaga hacia la izquierda, es: y(x, t) = A cos(kx+ ωt+ α).

2.2. Densidades de energıa cinetica, potencial, energıa mecanica y

potencia transmitida por la onda en un punto de una cuerda y

en un instante dado

1. Densidad de energıa cinetica: Para un trozo pequeno de la cuerda, de longitud ∆x, la energıa cinetica

es: ∆Ec(x, t) =µ∆x

2

(

∂y

∂t(x, t)

)2

.

La densidad de energıa cinetica por unidad de longitud vale: ηc(x, t) =∆Ec

∆x(x, t) =

µ

2

(

∂y

∂t(x, t)

)2

.

Como se puede ver, la ecuacion de ondas procede de aproximaciones a orden uno y la energıa es unaaproximacion de orden dos.

2. Densidad de energıa potencial: Para un trozo pequeno de cuerda, la energıa potencial se define comola diferencia de energıa entre la cuerda deformada y la cuerda sin deformar. Teniendo en cuenta lasexpresiones dadas al principio, queda:

∆U(x, t) = T

√

1 +

(

∂y

∂x(x, t)

)2

− 1

∆x ⇒ ∆U(x, t) ≈T∆x

2

(

∂y

∂x(x, t)

)2

La densidad de energıa potencial por unidad de longitud vale: ηP (x, t) =∆U

∆x(x, t) =

T

2

(

∂y

∂x(x, t)

)2

3. Densidad de energıa mecanica: Es la suma de las densidades de energıa potencial y de energıa cinetica.

4. Potencia transmitida por un punto de la cuerda: Se calcula a partir de la expresion: P = W = ~F ·~v,que da la potencia suministrada por la fuerza resultante a una partıcula en movimiento. En este caso lafuerza es la ejercida por el punto sobre la cuerda, que es igual y de signo contrario a la que hace la cuerda

sobre el punto. En este caso ~v es la velocidad vertical de oscilacion∂y

∂t(x, t)~j. La expresion para la potencia

transmitida es:

P = W = ~F · ~v = −T∂y

∂x(x, t)

∂y

∂t(x, t)

2.3. Ondas estacionarias en una cuerda de longitud finita

En una cuerda de longitud finita se forman unas ondas que no se propagan llamadas ondas estacionarias.La forma de estas ondas depende de las condiciones de contorno, es decir, de como estan los extremos de lacuerda.

10 Ondas

Un extremo de una cuerda puede estar fijo. En este caso su deformacion y todas las derivadas temporales deesta seran nulas en el, en todo instante porque no se mueve. Si xF representa el extremo fijo e y(x, t) representala deformacion de la cuerda, esta condicion se expresa mediante las ecuaciones:

y(xF , t) = 0 and∂ny

∂tn(xF , t) = 0, ∀t ≥ 0, ∀n ≥ 1

Un extremo puede tambien estar libre, es decir, su movimiento no esta sujeto a ninguna restriccion. Si xL

representa el extremo libre e y(x, t) representa la deformacion de la cuerda, la condicion, que se debe cumpliren este punto, se expresa mediante las ecuaciones:

∂y

∂x(xL, t) = 0 ∀t ≥ 0

Para usar ambas posibilidades, se va a considerar una cuerda, cuyo inicio, xF = 0, esta fijo y cuyo extremoxL = L esta libre. Por comodidad, se va a trabajar en complejos.

La solucion general es de la forma:

y(x, t) = A1ei(kx−ωt) +A2e

−i(kx+ωt)

A1 y A2 son constantes, en general complejas.

Se usa ahora y(0, t) = 0.

A1e−iωt) +A2e

−iωt = 0; ∀t ≥ 0 ⇒ A1 +A2 = 0 ⇒ y(x, t) = A1e−iωt

(

eikx − e−ikx)

⇒

y(x, t) = 2A1ie−iωt sin(kx)

Si se hace 2A1 = Ae−iβ , con A modulo del complejo y β su fase, se tiene:

y(x, t) = Aie−i(ωt+β) sin(kx) ⇒ y(x, t) = A sin(ωt+ β) sin kx

Quedan por determinar k, β,A y ω. Cuando se conozca k, ω quedara determinada por ω = kc, dado que cviene dada por las propiedades de la cuerda T y µ.

Para determinar k, se usa la otra condicion de contormo:∂y

∂x(L, t) = 0.

∂y

∂x(L, t) = 0 ⇒ Ak sin(ωt+ β) cos kL = 0 ⇒ cos kL = 0

Esta ultima ecuacion tiene infinitas soluciones, a cada una de las cuales corresponden un numero de ondas kn

y una frecuencia ωn diferentes, que son:

knL = (2n− 1)π

2; con n = 1, . . . , N, . . . ⇒ kn =

(2n− 1)π

2L; con n = 1, . . . , N, . . .

Cada solucion yn(x, t) asociada a un valor de n se denomina un armonico o un modo normal. El armonico cony1(x, t) se llama armonico fundamental porque todos los demas numeros de onda son multiplos enteros del suyoy todas las demas frecuencias son multiplos enteros de la suya. La forma general de un modo normal es:

yn(x, t) = An sin

(

(2n− 1)πct

2L+ βn

)

sin(2n− 1)πx

2L; con n = 1, . . . , N, . . .

El conjunto de costantes (An, βn)n=1,...,N,...) no se han determinado. Para hacerlo es necesario conocer los

valores iniciales de la onda y(x, 0); x ∈ [0, L] y la velocidad de oscilacion∂y

∂x(x, 0); x ∈ [0, L], ya que

la ecuacion de ondas contiene una derivada segunda respecto al tiempo. Conocidas estas dos funciones, losarmonicos se determinan completamente mediante la transformacion de Fourier, que queda totalmente fueradel alcance de este curso. Desde ahora se centrara la atencion en problemas relacionados con las propiedades delos armonicos.

2.3.1. Nodos y vientres

Nodo: Un nodo es un punto de la cuerda que esta siempre en reposo. Si xN es su abscisa, y(xN , t) = 0; ∀t.

Vientre: Un vientre es un punto de la cuerda cuya energıa potencial es nula en todo instante o tambien,cuya deformacion siempre alcanza el valor maximo.

Ondas 11

1. Ejemplo: Calcular los nodos del modo n de la cuerda vista anteriormante.

Para que en un punto xj haya un nodo de yn(x, t), se debe cumplir:

yn(xj , t) = 0; ∀t ⇒ sin(2n− 1)πxj

2L= 0 ⇒ xj =

2L

2n− 1j; con j = 0, . . . , n− 1

El armonico fundamental solo tiene un nodo: el origen de la cuerda. Para un modo n la distancia entredos nodos consecutivos vale:

xj+1 − xj =2L

2n− 1

2. Ejemplo: Calcular los vientres del modo n de la cuerda vista anteriormante.

Para que en un punto xl haya un vientre de yn(x, t), se debe cumplir:∣

∣

∣

∣

sin(2n− 1)πxl

2L

∣

∣

∣

∣

= 1 =⇒ xl =(2l− 1)L

(2n− 1)con l = 1, . . . , n

El armonico fundamental tiene un solo vientre en el extremo libre x = L. Para un modo n la distanciaentre dos vientres consecutivos vale:

xl+1 − xl =2L

2n− 1

Como se puede ver es el mismo valor que el de la distancia entre dos nodos consecutivos. Esto induce apensar que ambas distancias estan relacionadas con alguna propiedad intrınseca de la onda.

3. Ejemplo: Longitud de onda de la onda estacionaria del Ejemplo 1.

Antes se ha visto que:

kn =(2n− 1)π

2Lademas kn =

2π

λn⇒ L =

(2n− 1)λn

4⇐⇒ λn =

4L

2n− 1

Por tanto, para una cuerda de longitud L, con un extremo fijo y otro libre, La longitud debe ser unmultiplo impar de la cuarta parte de la longitud de onda. Ası para n = 1 la longitud de onda es cuatroveces la longitud de la cuerda.

Tambien la distancia entre dos vientres consecutivos o entre dos nodos consecutivos es la mitad de lalongitud de onda. Esta propiedad se cumple para todas las ondas estacionarias, independientemente delas condiciones de contorno e iniciales.

2.3.2. Energıa cinetica, potencial, mecanica en una onda y potencia transmitida

por un punto en el caso de una onda estacionaria

1. Energıa cinetica: Como se ha visto antes la densidad de energıa cinetica es:

ηc(x, t) =µ

2

(

∂y

∂t(x, t)

)2

La funcion de onda de una onda estacionaria es de la forma: yn(x, t) = An sin(ωnt + βn) sin knx. Ladensidad de energıa cinetica sera:

ηc(x, t) =µ

2A2

nω2n cos2(ωnt+ βn) sin2 knx

En las magnitudes periodicas interesa mas su valor medio en un periodo que su valor instantaneo. Paracalcular su densidad de energıa cinetica media en un periodo, se integra ηc(x, t) con respecto a t y sedivide por el valor del periodo T . El valor final es:

ηc(x) =µ

4A2

nω2n sin2 knx

Como se puede ver, la densidad de energıa cinetica media en un periodo depende del punto considerado.Sera nula en un nodo y maxima en un vientre. La energıa cinetica se calcula integrando la densidad mediaentre 0 y L. Su valor es:

12 Ondas

Ecin =µL

8A2

nω2n =

mA2nω

2n

8

2. Energıa potencial: Como se ha visto antes la densidad de energıa potencial es:

ηP (x, t) =T

2

(

∂y

∂x(x, t)

)2

La funcion de onda de una onda estacionaria es de la forma: yn(x, t) = An sin(ωnt + βn) sin knx. Ladensidad de energıa potencial sera:

ηP (x, t) =T

2A2

nk2n sin2(ωnt+ βn) cos2 knx

Para calcular su densidad de energıa potencial media en un periodo, se integra ηP (x, t) con respecto a ty se divide por el valor del periodo T . El valor final es:

ηP (x) =T

4A2

nk2n cos2 knx

T = c2µ y ωn = knc =⇒ ηP (x) =µA2

nω2n

4cos2 knx

La densidad media de energıa potencial en un periodo depende tambien del punto, es maxima en los nodosy nula en los vientres. Le energıa potencial total vale:

EPot =µL

8A2

nω2n =

mA2nω

2n

8

es decir, coincide con la cinetica.

3. Energıa mecanica: Como se ha visto antes la densidad de energıa mecanica es la suma de densidad deenergıa potencial y de la de energıa cinetica. Pasando por alto sus valores instantaneos en un punto, sevan a considerar sus valores medios en un periodo. Por los dos apartados anteriores, se tiene:

ηE(x) = ηc(x) + ηP (x) =µA2

nω2n

4

(

sin2 knx+ cos2 knx)

⇒ ηE(x) =µA2

nω2n

4

La densidad media temporal de energıa mecanica es la misma en todos los puntos de la cuerda. La energıatotal vale:

E =mA2

nω2n

4

y no varıa con el tiempo. Se trata de un sistema conservativo.

4. Potencia transmitida por un punto: Aplicando la expresion obtenida antes a la onda estacionariayn(x, t) = An sin(ωnt+ βn) sin knx, se obtiene la expresion:

P = W = −TA2nωnkn cos(ωnt+ βn) sin(ωnt+ βn) cos knx sin knx

Este valor instantaneo es cero en los nodos, se anula∂y

∂t, y en los vientres, se anula

∂y

∂x. En los demas

puntos es distinto de cero en salvo cuando la cuerda esta en posicion horizontal. Si dado un punto fijo secalcula la potencia media transmitida en un periodo, el resultado es cero. La potencia va en uno y otrosentido de forma que al cabo de un periodo, no se ha transmitido nada. Este es un argumento mas queprueba que las ondas estacionarias no se propagan.

2.4. Ondas armonicas que se propagan en una cuerda

Una vez vistas las ondas estacionarias, se van a ver las ondas que se propagan en una cuerda. Se supone, porcomodidad, que avanzan hacia la derecha. Su funcion de onda es:

y(x, t) = A cos(kx− ωt+ α)

Ondas 13

2.4.1. Energıa cinetica, potencial y mecanica en una onda que se propaga

1. Energıa cinetica: Como se ha visto antes la densidad de energıa cinetica es:

ηc(x, t) =µ

2

(

∂y

∂t(x, t)

)2

=µA2ω2

2sin2(kx− ωt+ α)

Su valor medio en un periodo es:

ηc(x) =µA2ω2

4; ∀x ∈ [0, L]

Este valor medio coincide con el valor medio por unidad de longitud. Para verlo basta integrar respecto ax entre 0 y λ y dividir por λ. La energıa cinetica sera por tanto:

Ec =mA2ω2

4

siendo m la masa de la cuerda.

2. Energıa potencial: Como se ha visto antes la densidad de energıa potencial es:

ηP (x, t) =T

2

(

∂y

∂x(x, t)

)2

=TA2k2

2sin2(kx− ωt+ α)

Teniendo en cuenta que T = µc2 y ω = ck, queda:

ηP (x, t) =µA2ω2

2sin2(kx− ωt+ α)

que coincide con la densidad de energıa cinetica. Las densidades de energıa cinetica y potencial son iguales

para toda onda armonica que se propaga en una cuerda. Este resutado se puede generalizar a cualquieronda transversal que se propaga en una cuerda.

El valor de la energıa potencial transportada por la onda es igual al de la energıa cinetica.

3. Energıa mecanica: El valor de la densidad de energıa mecanica es el doble de la de energıa cinetica ypor tanto la energıa de la onda es:

E =mA2ω2

2

siendo m la masa de la cuerda.

2.4.2. Potencia transmitida por un punto de una onda que se propaga

La expresion es la misma que la usada anteriormente. Si se considera un onda que se propaga hacia la derecha sufuncion de onda es de la forma ϕ(x−ct). La componente vertical de la fuerza, que ejerce el punto x sobre la cuerda,

es −T∂y

∂x(x, t) = −T

dϕ

du

∂u

∂xdonde u = x− ct y la velocidad de oscilacion es

∂y

∂t(x, t) =

dϕ

du

∂u

∂t= −c.

La potencia transmitida es:

W = Tc

(

dϕ

du

)2

Como puede verse la transmision es positiva, es decir, va en el mismo sentido que la propagacion.

Si ahora se considera una onda que se propaga en sentido negativo Ψ(x+ ct), haciendo v = x+ ct, se tiene parala potencia transmitida la expresion:

W = −Tc

(

dΨ

dv

)2

Como puede verse la transmision es negativa, es decir, va en el mismo sentido que la propagacion.

En general: la propagacion de la onda y la transmision de potencia van en el mismo sentido.

14 Ondas

En el caso de una onda armonica, se tiene: y(x, t) = A cos(kx∓ ωt+ α). El signo − corresponde a propagacionhacia la derecha y el + hacia la izquierda. La potencia instantanea, en el punto x y el instante t, es:

P (x, t) = W (x, t) = ±T k ω A2 sin2(kx∓ ωt+ α)

Para calcular la potencia media transmitida en un periodo, se integra la potencia entre 0 y T y se divide laintegral por T , el resultados es:

P = ¯W = ±TkωA2

2= ±

µc2kωA2

2=⇒ P = ¯W = ±

µA2ω2

2c

El signo + corresponde a propagacion hacia la derecha y el − hacia la izquierda.

2.5. Impedancia de una cuerda

La impedancia de una cuerda a las ondas transversales, cuando no hay disipacion de energıa, esta determinadapor dos parametros relacionados con el almacenamiento de energıa, inercia y elasticidad y ademas sera real.Este es el caso de las ondas trnsversales vistas aquı.

La impedancia de una cuerda viene dada por:

Z =Fuerza transversal

velocidad transversal=

∣

∣

∣

∣

∣

T ∂y∂x

∂y∂t

∣

∣

∣

∣

∣

Si la onda es del tipo y(x, t) = Aei(kx±ωt), su impedancia es:

Z =Tk

ω=µc2k

ω= µc

Las dimensiones de esta impedancia sonmasa

tiempo. Por esta razon en el sistema internacional se mide en

Kg

s.

2.6. Cambio de medio: reflexion y transmision de ondas en el con-

torno de una cuerda

Una cuerda, en rojo en la figura, esta formada por dos materiales diferentes y sus dos partes se unen en x = 0.A la izquierda esta el medio 1, la cuerda esta formada por un material y al derecha el 2. La frecuencia es iguala ambos lados, ya que no se crean ni se destruyen ondas, sin embargo la densidad es diferente a ambos ladosdel eje y y por lo tanto, tambien lo son los numeros de ondas y las velocidades de propagacion. La deformacionde la cuerda en x = 0 es la misma a ambos lados en todo instante, la cuerda no se rompe. La tension tienela misma componente horizontal, pero de signo contrario, a ambos lados y la componente vertical debe ser lamisma, en caso contrario la cuerda acabarıa por romperse.

1 2

X

YIncidente

Reflejada

Transmitida

Ondas 15

En el medio 1 estan superpuestas las ondas incidente y reflejada, que constituyen y1(x, t) = yi(x, t) + yR(x, t),y en el medio 2 esta la onda y2(x, t) que se transmite.

Las condiciones en x = 0 son

y1(0, t) = y2(0, t)

T∂y1∂x

(0, t) = T∂y2∂x

(0, t)

Haciendo: yi(x, t) = A1ei(k1x−ωt), yR(x, t) = B1e

−i(k1x+ωt) y y2(x, t) = A2ei(k2x−ωt), se tiene:

A1 + B1 = A2

k1 (A1 − B1) = k2A2

Si ahora se expresan las k en funcion de las impedancias kj =ω

cjy se tiene en cuenta que Zj =

T

cj, se obtiene:

kj =Zjω

T, que se sustituye en las ecuaciones de las amplitudes y se obtienen los siguientes coeficientes:

Coeficiente de reflexion de amplitudes = RA =B1

A1=Z1 − Z2

Z1 + Z2

Coeficiente de transmision de amplitudes = TA =A2

A1=

2Z1

Z1 + Z2

Casos posibles

Z2 < Z1 ⇒ B1 y A1 mismo signo, A2 > A1, hay reflexion sin cambio de fase.

Z2 = Z1 ⇒ B1 = 0, A2 = A1 la cuerda es igual a ambos lados, no hay reflexion y la onda no se altera.

Z2 > Z1 ⇒ B1 y A1 distinto signo, A2 < A1, hay reflexion con cambio de fase.

Z2 → ∞ ⇒ A2 → 0, B1 → −A1, reflexion total con cambio de signo.

2.6.1. Coeficientes de transmision y reflexion para la energıa

Al punto en el que tiene lugar el cambio de medio, llega una potencia: ¯Wi =µ1ω

2A21c1

2=Z1A

21ω

2

2, la onda

reflejada transporta: ¯WR =µ1ω

2B21c1

2=Z1B

21ω

2

2y la onda transmitida al medio 2 transporta:

¯WT =µ2ω

2A22c2

2=Z2A

22ω

2

2

Coeficiente de transmision de energıa = TE =¯WT

¯Wi

=4Z1Z2

(Z1 + Z2)2.

Coeficiente de reflexion de energıa = RE =¯WR

¯Wi

=(Z1 − Z2)

2

(Z1 + Z2)2.

Es facil comprobar que: RE + TE = 1 , de acuerdo con el principio de conservacion de la energıa.

Capıtulo 3

Ondas longitudinales en gases: ondas

sonoras

Ondas 17

3.1. Ondas longitudinales en un tubo cilındrico lleno de un gas

ideal

Se tiene un tubo cilındrico de seccion circular uniforme, S, que esta lleno de un gas ideal (p. ej. aire), que esta enequilibrio a una presion P0, cuya densidad es ρ0 y cuya temperatura es T0. Se considera el gas, que en equilibrioocupa un volumen ∆V = S∆x.

P0 ρ0 P0

T0

∆x

Se hace vibrar un diapason en uno de los extremos del tubo. Ası se provocan compresiones y dilataciones a lolargo del tubo.El gas, que ocupaba antes ∆x, ahora ocupa ∆x+∆φ (si ∆φ > 0, hay una dilatacion y si ∆φ < 0,una compresion). La densidad, ρ(x, t), ahora no es constante, depende del punto y el instante. La perturbacionφ(x, t), desplazamiento de una “seccion” de gas de su posicion de equilibrio, tambien depende de x y t.

∆

P ρT

P +

x + ∆φ

∆P

La ecuacion, que cumple el desplazamiento en un punto x y en un instante t, es:

∂2φ

∂t2(x, t) = c2

∂2φ

∂x2(x, t)

siendo: c =

√

γRT0

M. Aquı γ es la constante adiabatica del gas, T0 la temperatura del equilibrio,R la constante

de los gases y M la masa molecular del gas. La intervencion de gamma se debe a que las ondas longitudinales seconsideran procesos adiabaticos porque, dada su frecuencia, el gas no tiene tiempo para intercambiar calor consu entorno. Las ondas son longitudinales porque la perturbacion φ es paralela a la velocidad de propagacion delas ondas. Las compresiones y dilataciones tienen lugar en la direccion en la que avanza la onda.

3.1.1. Demostracion de la ecuacion de ondas longitudinales en un gas

Para demostrar la ecuacion de las ondas longitudinales son necesarias dos ecuaciones basicas: la de conservacionde la masa del gas y la de la segunda ley de Newton.

1. Conservacion de la masa: ρ0S∆x = ρS(∆x+ ∆φ) ⇒ ρ0 ≈ ρ

(

1 +∆φ

∆x

)

≈ ρ

(

1 +∂φ

∂x

)

Como se ha visto en la introduccion general de ondas tanto las perturbaciones como todas sus deriva-das son pequenas. Aplicando Taylor a orden uno, se obtiene la expresion de la densidad en funcion deldesplazamiento:

ρ = ρ0

(

1 +∂φ

∂x

)−1

⇒ ρ ≈ ρ0

(

1 −∂φ

∂x

)

2. Segunda ley de Newton: La masa de gas es: ρ0∆xS. La velocidad de desplazamiento de este gas es:∆φ

∆t≈∂φ

∂t⇒

∂2φ

∂t2es su aceleracion. La segunda ley de Newton es:

ρ0S∆x∂2φ

∂t2= −S∆p ≈ −S∆x

∂p

∂x⇒ ρ0

∂2φ

∂t2= −

∂p

∂x

18 Ondas

El problema ahora es calcular∂p

∂x. La variable relacionada con x es el desplazamiento φ(x, t), que a su vez

esta relacionado con ρ(x, t). La densidad y la presion estan relacionadas a traves de la ecuacion del proceso, quetiene lugar en la formacion y propagacion de las ondas de presion. Si la relacion entre p y ρ en este procesose designa como p = p(ρ)proceso, se cumple:

−∂p

∂x= −

(

dP

dρ

)

proceso

∂ρ

∂x= ρ0

(

dP

dρ

)

proceso

∂2φ

∂x2(x, t).

Solo se van a considerar procesos en los que:

(

dP

dρ

)

proceso

> 0.

Para estos procesos se verifica:

∂2φ

∂t2(x, t) = c2

∂2φ

∂x2(x, t)

c =

√

(

dp

dρ

)

proceso

Para un proceso adiabatico se cumple:

pV γ = C ⇒ p =C

V γ; como ρ =

m

V⇒ p =

Cργ

mγ⇒ p = Cργ =⇒

dp

dρ=γCργ

ρ=γP0

ρ0=⇒

dp

dρ=γRT0

M=⇒ c =

√

γRT0

M

El modulo de compresibilidad y la velocidad de las ondas de presion.

Se ha visto que c =

√

(

dp

dρ

)

proceso

, ahora se va a calcular c de una forma diferente, muy frecuente en los libros

de texto y de problemas.(

dp

dρ

)

ad

=

(

dp

dV

)

ad

dV

dρ= −

V

ρ

(

dp

dV

)

ad

Esta expresion se ha obtenido teniendo en cuenta la relacion entre V y ρ y operando. Se define el modulo decompresibilidad adiabatica como:

Ba = −V

(

dp

dV

)

ad

Con esta definicion la velocidad de propagacion es: c =

√

Ba

ρ0. El calculo de Ba da γP0 y la velocidad c

coincide con la anterior.

3.2. Ecuaciones de las ondas acusticas para las demas magnitudes

del gas

Las perturbacion de cualquier magnitud, respecto a su valor de equilibrio, cumple, a primer

orden, la ecuacion de ondas

1. Velocidad de oscilacion v(x, t) =∂φ

∂t(x, t)

∂2v

∂t2(x, t) = c2

∂2v

∂x2(x, t)

2. Densidad ρ(x, t) (Aproximacion a orden 1)

Ondas 19

∂2ρ

∂t2(x, t) = c2

∂2ρ

∂x2(x, t)

3. Presion p(x, t)

∂2p

∂t2(x, t) = c2

∂2p

∂x2(x, t)

4. Temperatura T (x, t)

∂2T

∂t2(x, t) = c2

∂2T

∂x2(x, t)

En todas estas ecuaciones la velocidad de propagacion es:

√

γRT0

M

3.3. Relaciones de fase y amplitud entre las diversas perturbaciones

en una onda de presion

Las perturbaciones de todas las magnitudes, excepto el desplazamiento, estan en fase entre sı y

retrasadas enπ

2respecto al desplazamiento.

1. Velocidad de oscilacion y desplazamiento.

φ(x, t) = φmei(kx−ωt) y v(x, t) =

∂φ

∂t(x, t) =⇒ v(x, t) = −iωφme

i(kx−ωt) =⇒

v(x, t) = vmei(kx−ωt−π/2) y vm = φmω

2. Velocidad de oscilacion y presion.

v = vmei(kx−ωt−π/2) y ρ0

∂v

∂t(x, t) = −

∂p

∂x(x, t) =⇒

∂p

∂x(x, t) = iωρ0vme

i(kx−ωt−π/2) =⇒

p(x, t) =ρ0ωvm

kei(kx−ωt−π/2) =⇒ p(x, t) = pme

i(kx−ωt−π/2) y pm = ρ0vmc

3. Velocidad de oscilacion y densidad.

ρ = ρ0

(

1 −∂φ

∂x

)

⇒∂ρ

∂t= −ρ0

∂v

∂xy v(x, t) = vme

i(kx−ωt−π/2) =⇒

∂ρ

∂t(x, t) = −iρ0vmke

i(kx−ωt−π/2) =⇒ ρ(x, t) =ρ0vmk

ωei(kx−ωt−π/2) =⇒

ρ(x, t) = ρmei(kx−ωt−π/2) y ρm =

ρ0vm

c

4. Temperatura y densidad.

TTotal = T0 + T (x, t), ρTotal = ρ0 + ρ(x, t) y TTotal = Cργ−1Total =⇒

T0 + T (x, t) = C(

ρ0 + ρmei(kx−ωt−π/2)

)γ−1

⇒ T (x, t) ≈ C(γ − 1)ρm

ρ0ργ−10 ei(kx−ωt−π/2) ⇒

T (x, t) = T0(γ − 1)ρm

ρ0ei(kx−ωt−π/2) =⇒ T (x, t) = Tme

i(kx−ωt−π/2) y Tm = T0(γ − 1)ρm

ρ0

3.4. Potencia transportada por una onda sonora. Intensidad y sen-

sacion sonora

Como ya se ha visto la potencia transportada por una onda, dejando de lado su signo, es:

W (x, t) =∣

∣

∣

~F · ~vosc

∣

∣

∣ ; si p(x, t) = pm cos(kx− ωt) y v(x, t) = vm cos(kx− ωt) ⇒

W (x, t) = Spmvm cos2(kx− ωt) =⇒ ¯W =Spmvm

2

20 Ondas

Como pm = ρ0vmc la potencia media transportada por una onda sonora es:

¯W =Sρ0v

2mc

2

3.4.1. Intensidad.

Mas interesante que la potencia transportada por una onda sonora es la:Intensidad :La intensidad de una onda, en un punto x y un instante t, es la potencia transportada por la onda

por unidad de superficie en ese punto y ese instante.

I(x, t) =W

S(x, t) = ρ0v

2mc cos2(kx− ωt) =⇒ I =

ρ0v2mc

2=pmvm

2

3.4.2. Sensacion sonora, nivel de intensidad sonora

La sensacion fisiologica de fuerza de un sonido varıa logarıtmicamente con la intensidad de este. Como en todasensacion hay un valor umbral de intensidad, I0 = 10−12w/m2, por debajo del cual el oido medio no oye. Haytambien un valor maximo de intensidad Imax = 1w/m2, por encima del cual no se oye, se siente dolor. Lasensacion sonora,β entre estos valores se mide en decibelios dB y su escala viene dada por la expresion:

β = 10 log10

I

I0dB

El nivel de intensidad sonora es el valor de la intensidad para la que se oye y esta comprendido entre = 10−12w/m2

y 1w/m2. estos valores de intensidad sonora correponden a unos valores de los niveles de intensidad sonora entre0dB y 120dB.

3.5. Impedancia de una onda acustica

Por definicion:

Z =

∣

∣

∣

∣

∣

p

(

∂φ

∂t

)−1∣

∣

∣

∣

∣

=pm

vmcomo pm = ρ0vmc =⇒ Z = ρ0c

La impedancia se mide enKg

m2s, cuando se mide en el sistema internacional de unidades.

3.6. Densidades de energıa cinetica, potencial y mecanica

La densidad de energıa cinetica, energıa cinetica por unidad de volumen, es:

ρcin =ρ0

2

(

∂φ

∂t

)2

=ρ0v

2m

2sin2(kx− ωt), su valor medio en un periodo es: ρcin =

ρ0v2m

4

La densidad de energıa potencial, energıa potencial por unidad de volumen, tiene el mismo valor que lade energıa cinetica para una onda que se propaga.

La densidad de energıa mecanica, energıa mecanica por unidad de volumen, su valor es dos veces el de ladensidad de energıa cinetica, para una onda que se propaga.

3.7. Ondas esfericas

Se va a calcular la ecuacion de una onda esferica de dos maneras. Una mediante razonamiento basado en laconservacion de la energıa y la otra obteniendo la ecuacion de una onda esferica.

Ondas 21

R2

R1O

1. Conservacion de la energıa: Se considera un emisor puntual, O, en un espacio homogeneo e isotropo.Las ondas que emite son superficies esfericas, que van alejandose del punto. Como no hay absorcion deenergıa, a todas las superficies esfericas llega la misma potencia. Si se consideran las superficies de radiosR1 y R2, se verifica:

W1 = W2 = W =⇒ W (x, t) = Sρ0cv2m cos2(kx− ωt) es independiente del radio =⇒

ρ0cv2m14πR

21 = ρ0cv

2m24πR

22 =⇒ v2

m1R21 = v2

m2R22; ∀vm y ∀r =⇒ vm =

Av

r

En este caso la amplitud de la velocidad debe ser una constante, propia de la velocidad, dividida porla distancia al foco emisor. Lo mismo debe ocurria con todas las magnitudes de esta onda sonora, quecumplan la ecuacion de ondas. Ası las ecuaciones de onda son de la forma:

a) Desplazamiento: φ(r, t) =Aφ

rf(r−ct) y para una onda armonica φ(r, t) =

Aφ

rcos(kr − ωt+ α+

π

2) .

b) Velocidad de oscilacion: v(r, t) =Av

rf(r − ct) y para una onda armonica:

v(r, t) =Av

rcos(kr − ωt+ α) .

c) Perturbacion de la presion de equilibrio: p(r, t) =Ap

rf(r − ct) y para una onda armonica:

p(r, t) =Ap

rcos(kr − ωt+ α) .

d) Perturbacion de la densidad de equilibrio: ρ(r, t) =Aρ

rf(r − ct) y para una onda armonica:

ρ(r, t) =Aρ

rcos(kr − ωt+ α) .

e) Perturbacion de la temperatura de equilibrio: T (r, t) =AT

rf(r−ct) y para una onda armonica:

T (r, t) =AT

rcos(kr − ωt+ α) .

2. Ecuacion para las ondas esfericas: Un onda esferica viene caracterizada por una funcion de onda

f(r, t), que solo depende de la distancia al foco emisor, r, y del tiempo, t. Siendo r =√

x2 + y2 + z2. Suecuacion en coordenadas cartesianas es:

22 Ondas

∂2f

∂x2(r, t) +

∂2f

∂y2(r, t) +

∂2f

∂z2(r, t) =

1

c2∂2f

∂t2(r, t)

Ahora se cambia de variables la ecuacion, se pasa de (x, y, z) → (r, t). Para ello se empieza por∂f

∂x.

∂f

∂x(r, t) =

∂f

∂r(r, t)

∂r

∂x=x

r

∂f

∂r(r, t) ⇒

∂2f

∂x2(r, t) =

x2

r2∂2f

∂r2(r, t) +

∂f

∂r(r, t)

(

1

r−x2

r3

)

∂f

∂y(r, t) =

∂f

∂r(r, t)

∂r

∂y=y

r

∂f

∂r(r, t) ⇒

∂2f

∂y2(r, t) =

y2

r2∂2f

∂r2(r, t) +

∂f

∂r(r, t)

(

1

r−y2

r3

)

∂f

∂z(r, t) =

∂f

∂r(r, t)

∂r

∂z=z

r

∂f

∂r(r, t) ⇒

∂2f

∂z2(r, t) =

z2

r2∂2f

∂r2(r, t) +

∂f

∂r(r, t)

(

1

r−z2

r3

)

Si se suman ahora las derivadas segundas y se tiene en cuenta la ecuacion de la onda sonora esferica, queda:

∂2f

∂r2(r, t) +

2

r

∂f

∂r(r, t) =

1

c2∂2f

∂t2(r, t) =⇒ c2

∂2(rf)

∂r2(r, t) =

∂2(rf)

∂t2(r, t)

Esta es una ecuacion de ondas para el producto rf(r, t) cuya solucion es de la forma:

f(r, t) =1

rϕ(r − ct)

y f(r, t) =1

rAf cos(kr − ωt+ α)

si es una onda armonica.

3.8. Condiciones de contorno en tubos sonoros

En un extremo abierto de un tubo, la perturbacion de la presion es nula, este extremo es un nodo de la presion.En un extremo cerrado la sobrepresion alcanza un maximo en valor absoluto. Ası la perturbacion de la presiontiene un nodo en un extremo abierto y un vientre en uno cerrado.

El desplazamiento es maximo en valor absoluto en un extremo abierto y nulo en un extremo cerrado. Tiene unvientre en un extremo abierto y un nodo en uno cerrado.

3.8.1. Coeficientes de transmision y reflexion para la velocidad de oscilacion y la

presion

Cuando una onda sonora llega a una superficie que separa dos medios de impedancias acusticas distintas, hayque tener en cuenta dos condiciones de contorno, al considerar la reflexion y transmision de la onda. Estasson:

1. -La velocidad de oscilacion: φi + φr = φt.

2. -La perturbacion de la presion: pi + pr = pt.

Donde el subındice i indica incidente, r reflejada y t transmitida.

φi + φr = φt ⇒ vmi + vmr = vmt.pi + pr = pt ⇒ Zivmi − Zivmr = ZDvmt

Aquı se obtiene para la velocidad de desplazamiento:

RAv=Zi − ZD

Zi + ZDy TAv

=2Zi

Zi + ZD.

y para las amplitudes de la presion:

pr = −Zivmr y las ecuaciones anteriores RAp= −RAv

y TAp= TAv

ZD

Zi=⇒

Ondas 23

RAp=Zi − ZD

Zi + ZDy TAp

=2ZD

Zi + ZD

3.8.2. Coeficientes de transmision y reflexion para la energıa

La relacion entre la energıa transmitida y la incidente es la mima que la relacion entre la intensidad transmitiday la incidente. El coeficiente de transmision para le energıa es:

TE =ItIi

=ρDcDv

2mD

ρiciv2mi

=ZD

Zi

(

2Zi

Zi + ZD

)2

=⇒ TE =4ZiZD

(Zi + ZD)2

Analogamente la relacion entre la energıa reflejada y la incidente es la misma que entre la intensidad reflejaday la incidente. El coeficiente de reflexion para le energıa es:

RE =IrIi

=v2

mr

v2mi

=⇒ RE =

(

Zi − ZD

Zi + ZD

)2

Apendice A

Apendice

Ondas 25

A.1. Integracion de funciones trigonometricas

En las partes siguientes del curso se usaran integrales definidas, entre 0 y su periodo, de funciones trigonometricasy sus cuadrados. Por esta razon se va a dar aquı un resumen de como calcularlas.

A.1.1. Formas directas

Las formas directas son:∫ 2π

0

sinϕdϕ,

∫ 2π

0

cosϕdϕ,

∫ 2π

0

sin2 ϕdϕ,

∫ 2π

0

cos2 ϕdϕ,

∫ 2π

0

cosϕ sinϕdϕ

∫ 2π

0

cosϕ cosαdϕ

1.

∫ 2π

0

sinϕdϕ = [−cosϕ]2π0 = cos 0 − cos 2π = 0

2.

∫ 2π

0

cosϕdϕ = [sinϕ]2π0 = 0

3.

∫ 2π

0

sin2 ϕdϕ .

Para resolver esta integral hay que usar dos igualdades trigonometricas.

cos2 ϕ+ sin2 ϕ = 1

cos2 ϕ− sin2 ϕ = cos 2ϕ

De este sistema se deduce:

sin2 ϕ =1

2−

1

2cos 2ϕ ⇒

∫ 2π

0

sin2 ϕdϕ =1

2

∫ 2π

0

(1 − cos 2ϕ) dϕ =⇒

∫ 2π

0

sin2 ϕdϕ = π

1

2π

∫ 2π

0

sin2 ϕdϕ =1

2

4.

∫ 2π

0

cos2 ϕdϕ . Del sistema de ecuaciones del apartado anterior, se deduce tambien:

cos2 ϕ =1

2+

1

2cos 2ϕ ⇒

∫ 2π

0

cos2 ϕdϕ =1

2

∫ 2π

0

(1 + cos 2ϕ) dϕ =⇒

∫ 2π

0

cos2 ϕdϕ = π

1

2π

∫ 2π

0

cos2 ϕdϕ =1

2

5.

∫ 2π

0

cosϕ sinϕdϕ =1

2

∫ 2π

0

sin 2ϕdϕ = 0 .

6.

∫ 2π

0

cosϕ cosαdϕ = cosα

∫ 2π

0

cosϕdϕ = 0

A.1.2. Expresiones usadas en ondas estacionarias

Sea la onda estacionaria yn(x, t) = An sin(ωnt+ βn) sin knx . Se quiere calcular su densidad de energıa cineticamedia en un periodo, su densidad de energıa potencial media en un periodo y su densidad media de energıamecanica en un periodo y tambien la potencia media transmitida por un punto en un periodo.

1. Densidad media de energıa cinetica en un periodo: La densidad de energıa cinetica en un puntox y un instante t vale:

ηc(x, t) =µA2

nω2n

2cos2(ωnt+ αn) sin2 knx

26 Ondas

Para hacer la integral

∫ Tn

0

cos2(ωnt+ αn)dt, se hace el cambio: ωnt+ αn = φn.

ωnt+ αn = φn ⇒ dt =dφn

ωn

Cuando t = 0, φn = βn y cuando t = Tn, φn = βn2π. Se va a calcular:1

Tn

∫ 2π

0

cos2(ωnt+ αn)dt.

1

Tn

∫ 2π

0

cos2(ωnt+ αn)dt =1

2π

∫ βn+2π

βn

cos2 φndφn =1

2

Ası se cumple:

ηc(x) =µA2

nω2n

4sin2 knx

2. Densidad media de energıa potencial en un periodo: La densidad de energıa potencial en un puntox y un instante t vale:

ηP (x, t) =TA2

nk2n

2sin2(ωnt+ αn) cos2 knx

Queda por resolver la integral:

∫ Tn

0

sin2(ωnt + αn)dt. Para ello se hace el cambio del apartado anterior

y se tiene:

1

Tn

∫ 2π

0

sin2(ωnt+ αn)dt =1

2π

∫ βn+2π

βn

sin2 φndφn =1

2

Ası se cumple:

ηP (x) =TA2

nk2n

4cos2 knx

teniendo en cuenta que T = µc2 y ωn = ckn queda:

ηP (x) =µA2

nω2n

4cos2 knx

3. Densidad media de energıa mecanica en un periodo: La densidad media de energıa mecanica enun periodo es:

ηE(x) = ηc(x) + ηP (x) =µA2

nω2n

4

(

sin2 knx+ cos2 knx)

⇒ ηE(x) =µA2

nω2n

4

4. Potencia media transmitida por un punto en un periodo:

P (x, t) = W (x, t) = −T∂y

∂x(x, t)

∂y

∂t(x, y) = Tknωn cos knx sin knx cos(ωnt+ αn) sin(ωnt+ αn) ⇒

P (x) = ¯W (x) = Tknωn cos knx sin knx1

Tn

∫ Tn

0

cos(ωnt+ αn) sin(ωnt+ αn) dt =⇒ P (x) = ¯W (x) = 0 .

A.1.3. Expresiones usadas en ondas armonicas que se propagan

Para la onda armonica que se propaga:

y(x, t) = A cos(kx∓ ωt+ alpha)

se van a calcular su densidad de energıa cinetica media en un periodo, su densidad de energıa potencial mediaen un periodo y su densidad media de energıa mecanica en un periodo y tambien la potencia media transmitidapor un punto en un periodo.

1. Densidad media de energıa cinetica en un periodo: La densidad de energıa cinetica en un puntox y un instante t vale:

Ondas 27

ηc(x, t) =µA2

nω2n

2sin2(kx∓ ωt+ alpha) ⇒ η(x) =

µA2nω

2n

2T

∫ T

0

sin2(kx∓ ωt+ α)dt.

Se hace: kx ∓ ωt + α = φ ⇒ dt = ∓dφ

ω. Cuando φ = kx + ωt + α los lımites de integracion son

φ = 2π + kx+ α y φ = kx+ α y la densidad es:

ηc(x) =µA2

nω2n

2

1

2π

∫ 2π+kx+α

kx+α

sin2 φdφ =⇒ ηc(x) =µA2

nω2n

4

Cuando φ = kx− ωt+ α, dt = −dφ

ωy los lımites de integracion son φ = −2π + kx+ α y φ = kx+ α. La

densidad es:

ηc(x) = −µA2ω2

2

1

2π

∫ −2π+kx+α

kx+α

sin2 φdφ =⇒ ηc(x) =µA2ω2

4

La densidad media en un periodo de energıa cinetica es constante en todos los puntos y vale: ηc(x) =µA2ω2

4

2. Densidad media de energıa potencial en un periodo: La densidad de energıa potencial en un puntox y un instante t vale:

ηP (x) =TA2k2

2

1

T

∫ T

0

sin2(kx∓ ωt+ α) dt =⇒ ηP (x) =TA2k2

4=µA2ω2

4; ∀x

La densidad media en un periodo de energıa potencial es constante en todos los puntos e igual a la densidad

media de enrgıa cinetica en un periodo, su valor es: ηP (x) =µA2ω2

4

3. Densidad media de energıa en un periodo: De acuerdo a lo calculado previamente la densidadmedia de energıa en un periodo vale:

η = ηc + ηP =µA2ω2

2

4. Potencia media transmitida por un punto en un periodo:

P (x, t) = W (x, t) = −T∂y

∂x(x, t)

∂y

∂t(x, y) = TkωA2 sin2(kx∓ωt+α) =⇒ P = ¯W =

TkωA2

2=µA2ω2

2c