TrigonometríaCristian Velandia M.Sc

Mapa de Navegación

Introducción

Razones Trigonométricas

Contenido

Razones Trigonométricas en Angulos

Ley de Seno

Autoevaluación

Ley Coseno

Objetivos

Conceptos Previos

TALLER – FUNCIONES

Objetivos

Al finalizar este módulo conocerás las razones trigonométricas y sus relaciones.

TALLER – FUNCIONES

“ Un Matemático es un Quijote moderno que

lucha en un mundo real con armas imaginarias “ …

Aplicarás las relaciones trigonométricas para el cálculo de distancias y ángulos en situaciones reales.

Utilizar los conocimientos geométricos para efectuar mediciones indirectas relacionadas con

situaciones tomadas de contextos cotidianos.

IntroducciónTALLER – FUNCIONES

Observa el área del triángulo formado por diferentes figuras geométricas …

¿Por qué cuando cambiamos el orden de las figuras, el área no es la misma?

IntroducciónTALLER – FUNCIONES

La trigonometría es una de las rama de las matemáticas que estudia las

relaciones entre los lados y los ángulos de los triángulos, siendo su significado etimológico “medida de triángulos”.

Una de las aplicaciones más interesantes de la trigonometría se realizan en Física, o en Ingeniería en el estudio de fenómenos

periódicos, por ejemplo en el flujo de corriente alterna para la ingeniería eléctrica.

El estudio de la trigonometría es muy interesante ya que te permite resolver

una gran cantidad de situaciones y problemas en el mundo real, resultando

fundamental especialmente en cualquier tipo de aplicación basada en

geometrías y distancias.

IntroducciónTALLER – FUNCIONES

Las primeras aplicaciones fueron en el área de la astronomía, la navegación y la

geodesia; casos donde NO es posible hacer mediciones de manera directa o donde las

distancias son inaccesibles, como la distancia de la Tierra a la Luna o la medida

del radio del Sol.

En este módulo descubrirás la aplicabilidad de la trigonometría para todo tipo de cálculos geométricos como la obtención de áreas,

medidas de lados y ángulos en figuras geométricas.

Durante el estudio de los módulos anteriores has ido adquiriendo

conocimientos de geometría analítica tales como ángulos, rectas, relaciones angulares, funciones trigonométricas, triángulos, circunferencia, teorema de

Pitágoras, etc,

Conceptos Previos

TALLER – FUNCIONES

Con el fin de iniciar nuestro estudio de trigonometría, analicemos los ángulos y

lados en un triángulo rectángulo:

Ahora observa cuando cambiamos el ángulo de referencia:

Ángulo

Observa que este lado es OPUESTO

al ángulo

Observa que este lado es cercano o

ADYACENTE al ángulo

Observa que el lado más largo e le llama

HIPOTENUSAÁngulo

Observa que este lado es ADYACENTE

al ángulo

Observa que este lado es cercano o

OPUESTO al ángulo

Observa que este es el lado más largo:

HIPOTENUSA

Es muy importante que tengas en claro el ángulo de referencia y los lados correspondiente.

Contenido

TALLER – FUNCIONES

TALLER – FUNCIONES

A continuación se hace una generalidad de los 3 temas que se analizaran en este taller:

TRIGONOMETRÍA

1. Razones Trigonométricas 2. Ley de Seno

3. Ley de Coseno

Cuando necesitas obtener las medidas desconocidas de lados

y ángulos en un triángulo rectángulo, puedes aplicar razones trigonométricas.

Cuando necesitas obtener las medidas desconocidas de lados y ángulos en cualquier tipo de triángulo, puedes aplicar la ley

de Seno.

Cuando necesitas obtener las medidas desconocidas de lados y

ángulos en cualquier tipo de triángulo, podemos aplicar la ley

de coseno.

a2 b2 c 2 2bc cosA

sen OpuestoHipotenusa

asen A

b

sen B

csen C

TALLER – FUNCIONES

Imagina que un joven skater requiere diseñar e implementar una rampa con

el fin de generear un salto determinado en una competencia.

Para lograrlo decide diseñar una rampa que tiene un

ángulo de elevación de 40 grados. Y la distancia de la

rampa debe ser de 1.5 metros.

1.5 m

40°

Para generar el análisis y obtener las medidas tanto de los ángulos y lados de la rampa, generemos un

dibujo de esta en dos dimensiones.

?

?

Ang = 40°

Observa que este lado es OPUESTO

al ángulo. No conocemos aún

la medida

Observa que este lado es cercano o ADYACENTE al ángulo de referencia No conocemos aun la medida.

Lado más largo o HIPOTENUSA = 1.5m

Razones Trigonométricas

TALLER – FUNCIONES

Con el fin de obtener las medidas de lados y ángulos en un triángulo rectángulo, podemos aplicar las siguientes

razones trigonométricas:

Para hallar la medida de los lados de la rampa, utilizamos las razones trigonométricas de la

siguiente manera:

Ahora para hallar el lado adyacente podemos utilizar la razón trigonométrica coseno o tangente

ya que tenemos ahora el dato de lado opuesto.

Lado OpuestoSeno (ángulo) =

Hipotenusa

Lado AdyacenteCoseno (ángulo) =

Hipotenusa

Lado OpuestoTangente ( ángulo) =

Lado Adyacente

Entonces para nuestra aplicación de la rampa obtenemos:

Ang = 40°

OPUESTO

ADYACENTE

HIPOTENUSA = 1.5m

Lado OpuestoSeno (ángulo) =

Hipotenusa

Lado OpuestoSeno (40°) =

1.5 m

Lado Opuesto(1.5) (0,642) =

Lado Opuesto0,964 m =

Lado AdyacenteCoseno (40) =

Hipotenusa

Lado AdyacenteCoseno (40) =

1.5

Lado Adyacente(1.5) ( 0,766) =

La función seno la obienes en la

calculador con la tecla sin y luego el

ángulo

Razones Trigonométricas en Ángulos

TALLER – FUNCIONES

Sabias que la Torre de Pisa perdió la posición vertical apenas comenzó a construirse en agosto de 1173. Tiene una altura de 55.8m y una distancia desde la parte mas alta al piso de aproximadamente 55m.

Altu

ra =

55.

8 m

Dist

anci

a =

55.4

mEl peso estimado es de 14.700 toneladas. Posee 8 niveles; la base está decorada con arcos ciegos de 15 columnas. Los 6 niveles siguientes presentan columnata externa y está rematada por un campanario. La Torre tiene una escalera de espiral interna con 294 escalones.

Te gustaría saber ¿Cuál es el ángulo de inclinación de la Torre? Puedes aplicar las diferentes razones trigonométricas y hallar la función inversa con el fin de obtener el ángulo, tal como se muestra a continuación:

Ángulo

Lado AdyacenteCoseno (ángulo) =

Hipotenusa

55.6 mCoseno (ángulo) =

55.8 m

Coseno (ángulo) = 0.996

Coseno (ángulo) = 0.996

Con el fin de hallar el ángulo de inclinación aplicamos la función inversa de coseno: Arcoseno.

ángulo = Cos-1 ( 0.996 )

ángulo = 5.1 grados

La función arcoseno la obienes en la calculadora con shift coseno o segunda función seno.

14.5 m

53° ?

Se requiere delimitar un área triangular para aislar un perro labrador. La distancia desde la casa del hombre hasta el árbol es de 14.5 metros y el ángulo que forma este cable con la cerca del lote es de 53°. ¿Cuál es la distancia entre las casas y el árbol?

Ejercicio razones Trigonométricas

TALLER – FUNCIONES

Para la solución de este ejercicio cuentas con 2 minutos

?

Solución Ejercicio razones Trigonométricas

TALLER – FUNCIONES

Para la solución de este ejercicio graficamos el siguiente triángulo:

53°

OPUESTO

ADYACENTE

14.5m

Lado OpuestoSeno (ángulo) =

Hipotenusa

Lado OpuestoSeno (53°) =

14.5 m

Lado Opuesto(14.5) (0,79) =

Lado Opuesto11.5 m =

Para hallar la medida de los otros lados podemos utilizar la razón trigonométrica

coseno o tangente:

Lado OpuestoTangente ( ángulo) =

Lado Adyacente

11.5Tangente ( 53° ) =

Lado Adyacente

11.5( 1.32 ) =

Lado Adyacente

11.5

( 1.32 )Lado Adyacente =

Despejamos la variable del lado adyacente. Pasamos esta variable a multiplicar y el valor de

tangente de 53 a dividir:

8.71 mLado Adyacente =

Ley de Seno

TALLER – FUNCIONES

Recuerda que en el inicio de este módulo citamos que las razones trigonométricas se aplican solamente en triángulos rectángulos

(triángulos con un ángulo de 90 grados).

En cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo

opuesto es constante.

La ley de senos establece la siguiente relación entre ángulos y lados:

No todos los triángulos poseen un ángulo recto (90º). Aquellos triángulos que no

poseen un ángulo recto se les llama triángulos oblicuángulos.

cCsen

bBsen

aAsen

asen A

b

sen B

csen C

Esta ley se puede utilizar de esta forma y ofrece el mismo resultado final

Se tiene un triángulo oblicuángulo con las siguientes medidas: a = 6 m, B = 45° y C = 105°. Determina los

restantes elementos. Se conocen 2 ángulos y un lado por lo tanto se aplica la ley del seno.

A 180 (C B)A 180 105 45

A 30o

TALLER – FUNCIONES

Aplica la siguiente estrategia:

Recuerda que la suma de los ángulos internos de un triángulo es igual a 180. Por lo tanto para conocer el ángulo A debemos restar a 180 el ángulo B y C respectivamente.

6sen 30

b

sen 45

Ahora, con todos los ángulos aplicamos la ley de seno para hallar el lado b:

asen A

b

sen B

Remplazamos valores dada por la ley de seno:

6(sen 45) b(sen30)6(sen 45)(sen 30)

b

8.48 b

Despejamos la variable b de la ecuación:

Ejemplo

De la misma forma obtenemos el lado C

asen A

b

sen B

csen C

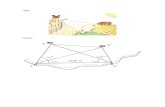
Para medir la longitud d de un lago, se estableció y se midió una línea de base AB de 125 metros. Los ángulos A y B son 41.6º y 124.3º, respectivamente.

¿Qué tan largo es el lago?12

5 m

Ejercicio de aplicación Ley de Seno

TALLER – FUNCIONES

Para la solución de este ejercicio cuentas con 2 minutos

Para medir la longitud d de un lago, se estableció y se midió una línea de base AB de

125 metros. Los ángulos A y B son 41.6º y 124.3º, respectivamente. ¿Qué tan largo es el lago?

125

m

1.14

9.165180)3.1246.41(180

)(180

C

CC

BAC

TALLER – FUNCIONES

Estrategia de solución:

Como nos dan la medida de un lado deberíamos conocer el ángulo en C para luego utilizar la ley de senos y encontrar

d. Recuerda que la suma de todos los ángulos internos de un triángulo son 180°.

6.41 1.14 125

send

sen

Ahora, aplicamos la ley de seno para hallar el lado d:

Asena

Csenc

Remplazamos valores dada por la ley de seno:

d

dsensen

sendsen

66.3401.14

)6.41 (125)1.14 ()6.41 (125

Despejamos la variable d de la ecuación:

Ley de Coseno

TALLER – FUNCIONES

Cuando NO tienes entre los datos un par de elementos opuestos, la ley de senos NO es suficiente. La ley de los Cosenos es una expresión que te permite conocer

un lado de un triángulo cualquiera, si conoces los otros dos y el ángulo opuesto al lado que quieres conocer. En 3 ecuaciones la ley de cosenos establece que:

Como te puedes dar cuenta la ley de cosenos se puede considerar como una extensión del teorema de Pitágoras y es

aplicable a todos los triángulos.

a2 b2 c 2 2bc cosA

b2 a2 c 2 2ac cosB

c 2 a2 b2 2abcosC

Paso 1: Utiliza la ley de cosenos para despejar b.

cmbb

Baccab

Baccab

96.54.32cos)45.6)(3.10(2)45.6()3.10(

cos2

cos2

22

22

222

TALLER – FUNCIONES

Obtener la medida del lado b y los ángulos α y θ del triángulo:

Ejercicio Ley de CosenoPaso 2: Utiliza la ley de senos para encontrar . Puesto que el lado c es más corto que el lado a, debe ser agudo.

44.35

96.5)4.32(45.6

)()()(

1

sensen

bsencsen

sencsenbsenb

senc

Paso 3: Calcular el tercer ángulo

16.112

)44.354.32(180)(180

TALLER – FUNCIONES

Ejercicio de Aplicación Ley de Coseno

52°

Obtener la distancia y los ángulos del campo de golf. Para ello cuentas con 2 minutos.

a

c

b

Paso 1: Utiliza la ley de cosenos para hallar la distancia a:

a2 b2 c 2 2bccosA

a b2 c 2 2bccosA

a (500)2 (420)2 2(500)(420)cos52

a 426400 258577.8a409.6m

TALLER – FUNCIONES

Ejercicio de Aplicación Ley de CosenoPaso 2: Utiliza la ley de senos para encontrar .

csen C

a

sen Ac(sen A) a(sen C)

sen C c(sen A)a

C sen 1 420(sen 52)409,6

C 54o

Paso 3: Calcular el tercer ángulo

B 180 (A C)B 180 (52 54)

B74o

52°

Obtener la distancia y los ángulos del campo de golf:

a

c

b

TALLER – FUNCIONES