Aplicaciãƒâ³n de funciones
-
Upload
gerardo-jueaerezz-aeguaeyoe -
Category
Documents
-
view
63 -
download
0
Transcript of Aplicaciãƒâ³n de funciones

Aplicacioacuten de funcionesQuiacutemica fiacutesica y biologiacutea
Integrantes
bullMa Esther Vaacutezquez MartiacutenezbullViacutector Vargas Torrescano
bullJesuacutes Gerardo Juaacuterez AguayobullAacutengel Giresse Ramos Rojas
USO DE DERIVADAS EN QUIacuteMICA A lo largo del tiempo la quiacutemica y las
matemaacuteticas han estado relacionadas dado que las aplicaciones matemaacuteticas sirven para crear modelos teoacutericos y expresiones para la mejor comprensioacuten de la quiacutemica
Auacuten maacutes en la quiacutemica las derivadas han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
INTRODUCCIOacuteN A LAS FUNCIONES A) DEFINICIOacuteN DE FUNCIOacuteN Una funcioacuten es una relacioacuten entre dos variables
numeacutericas X e Y de forma que a cada valor de X le corresponde un solo valor de y La variable X se llama variable independiente La variable Y se llama variable dependiente
B) DOMINIO Y RECORRIDO DE UNA FUNCIOacuteN f(x) Se llama dominio de una funcioacuten f(x) a todos los
valores de X para los que f(x) existe El dominio se denota como Dom(f)
Se llama recorrido o imagen de una funcioacuten f(x) a todos los valores que puede tomar f(x) La imagen se denota como Im(f)
1- FUNCION SOBRE PUNTO DE EBULLICION
A nivel del mar el punto de ebullicioacuten del agua es de 100 ordmC Cuando se asciende a una montantildea el punto de ebullicioacuten disminuye en funcioacuten de la altura con arreglo a la siguiente foacutermula t = 100 ndash 0001h Donde t es la temperatura del punto de ebullicioacuten en grados centiacutegrados y h la altura alcanzada en metros A) iquestCuaacutel es el punto de ebullicioacuten a 1500 m de
altitud
B)Realiza una grafica que represente la disminucioacuten del punto de ebullicioacuten en funcioacuten de la altura
SOLUCION Este procedimiento se puede realizar mediante la regla de 3 si observamos que al multiplicar la temperatura establecida al nivel del mar (que es 100 ordmc) en funcioacuten de la altura establecida (que es 0001h) y lo dividimos entre los 1500 metros de altura el resultado seraacute el punto de ebullicioacuten donde evidentemente cumple con lo establecido y disminuye considerablementeRESPUESTA6666666666666667e^-5
2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

USO DE DERIVADAS EN QUIacuteMICA A lo largo del tiempo la quiacutemica y las
matemaacuteticas han estado relacionadas dado que las aplicaciones matemaacuteticas sirven para crear modelos teoacutericos y expresiones para la mejor comprensioacuten de la quiacutemica
Auacuten maacutes en la quiacutemica las derivadas han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
INTRODUCCIOacuteN A LAS FUNCIONES A) DEFINICIOacuteN DE FUNCIOacuteN Una funcioacuten es una relacioacuten entre dos variables
numeacutericas X e Y de forma que a cada valor de X le corresponde un solo valor de y La variable X se llama variable independiente La variable Y se llama variable dependiente
B) DOMINIO Y RECORRIDO DE UNA FUNCIOacuteN f(x) Se llama dominio de una funcioacuten f(x) a todos los
valores de X para los que f(x) existe El dominio se denota como Dom(f)
Se llama recorrido o imagen de una funcioacuten f(x) a todos los valores que puede tomar f(x) La imagen se denota como Im(f)
1- FUNCION SOBRE PUNTO DE EBULLICION
A nivel del mar el punto de ebullicioacuten del agua es de 100 ordmC Cuando se asciende a una montantildea el punto de ebullicioacuten disminuye en funcioacuten de la altura con arreglo a la siguiente foacutermula t = 100 ndash 0001h Donde t es la temperatura del punto de ebullicioacuten en grados centiacutegrados y h la altura alcanzada en metros A) iquestCuaacutel es el punto de ebullicioacuten a 1500 m de
altitud
B)Realiza una grafica que represente la disminucioacuten del punto de ebullicioacuten en funcioacuten de la altura
SOLUCION Este procedimiento se puede realizar mediante la regla de 3 si observamos que al multiplicar la temperatura establecida al nivel del mar (que es 100 ordmc) en funcioacuten de la altura establecida (que es 0001h) y lo dividimos entre los 1500 metros de altura el resultado seraacute el punto de ebullicioacuten donde evidentemente cumple con lo establecido y disminuye considerablementeRESPUESTA6666666666666667e^-5
2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

INTRODUCCIOacuteN A LAS FUNCIONES A) DEFINICIOacuteN DE FUNCIOacuteN Una funcioacuten es una relacioacuten entre dos variables
numeacutericas X e Y de forma que a cada valor de X le corresponde un solo valor de y La variable X se llama variable independiente La variable Y se llama variable dependiente
B) DOMINIO Y RECORRIDO DE UNA FUNCIOacuteN f(x) Se llama dominio de una funcioacuten f(x) a todos los
valores de X para los que f(x) existe El dominio se denota como Dom(f)
Se llama recorrido o imagen de una funcioacuten f(x) a todos los valores que puede tomar f(x) La imagen se denota como Im(f)
1- FUNCION SOBRE PUNTO DE EBULLICION
A nivel del mar el punto de ebullicioacuten del agua es de 100 ordmC Cuando se asciende a una montantildea el punto de ebullicioacuten disminuye en funcioacuten de la altura con arreglo a la siguiente foacutermula t = 100 ndash 0001h Donde t es la temperatura del punto de ebullicioacuten en grados centiacutegrados y h la altura alcanzada en metros A) iquestCuaacutel es el punto de ebullicioacuten a 1500 m de
altitud
B)Realiza una grafica que represente la disminucioacuten del punto de ebullicioacuten en funcioacuten de la altura
SOLUCION Este procedimiento se puede realizar mediante la regla de 3 si observamos que al multiplicar la temperatura establecida al nivel del mar (que es 100 ordmc) en funcioacuten de la altura establecida (que es 0001h) y lo dividimos entre los 1500 metros de altura el resultado seraacute el punto de ebullicioacuten donde evidentemente cumple con lo establecido y disminuye considerablementeRESPUESTA6666666666666667e^-5
2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

1- FUNCION SOBRE PUNTO DE EBULLICION
A nivel del mar el punto de ebullicioacuten del agua es de 100 ordmC Cuando se asciende a una montantildea el punto de ebullicioacuten disminuye en funcioacuten de la altura con arreglo a la siguiente foacutermula t = 100 ndash 0001h Donde t es la temperatura del punto de ebullicioacuten en grados centiacutegrados y h la altura alcanzada en metros A) iquestCuaacutel es el punto de ebullicioacuten a 1500 m de
altitud
B)Realiza una grafica que represente la disminucioacuten del punto de ebullicioacuten en funcioacuten de la altura
SOLUCION Este procedimiento se puede realizar mediante la regla de 3 si observamos que al multiplicar la temperatura establecida al nivel del mar (que es 100 ordmc) en funcioacuten de la altura establecida (que es 0001h) y lo dividimos entre los 1500 metros de altura el resultado seraacute el punto de ebullicioacuten donde evidentemente cumple con lo establecido y disminuye considerablementeRESPUESTA6666666666666667e^-5
2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

SOLUCION Este procedimiento se puede realizar mediante la regla de 3 si observamos que al multiplicar la temperatura establecida al nivel del mar (que es 100 ordmc) en funcioacuten de la altura establecida (que es 0001h) y lo dividimos entre los 1500 metros de altura el resultado seraacute el punto de ebullicioacuten donde evidentemente cumple con lo establecido y disminuye considerablementeRESPUESTA6666666666666667e^-5
2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA En las 10 primeras semanas de cultivo de una
planta que mediacutea 2 cm
Se ha observado que su crecimiento es directamente proporcional al tiempo viendo que en la primera semana ha pasado a medir 25 cm
Establecer una funcioacuten a fin que deacute la altura de la planta en funcioacuten del tiempo y representar graacuteficamente
SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

SOLUCIOacuteN Con los datos obtenidos solo realizamos operaciones
Altura inicial = 2cm Crecimiento semanal = 25 minus 2 = 05 y= 05 x + 2
La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

La graacutefica muestra la variacioacuten de temperatura durante algunas horas de un diacutea de primavera en CracoviaDe acuerdo a la siguiente grafica determinar los incisos ABC Y D EJE X REPRESENTA TEMPERATURA EN Cordm
EJE Y REPRESENTATIEMPO EN HORAS
3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

3- FUNCION SOBRE VARIACION DE TEMPERATURAResponda las siguientes preguntas seguacuten la grafica mostradaA)iquestQueacute diacutea alcanzoacute la temperatura maacuteximaB)iquestCuaacutel fue esta temperaturaC)iquestEntre que 2 diacuteas se produce la variacioacuten maacutexima de temperaturaD)iquestCuaacutel es esta variacioacutenSOLUCIOacuteN A)La temperatura maacutexima se alcanzoacute el diacutea 5B) Esta temperatura fue de 395 ordmCC) La variacioacuten maacutexima de temperatura se produce entre el diacutea 4 y el diacutea 5D) Dicha variacioacuten es de 3 ordmC en efecto 395 minus 365 = 3 ordmC
SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

SUSTANCIAS RADIOACTIVAS Se ha comprobado que los isoacutetopos de los
elementos radiactivos presentan distintos grados de inestabilidad en el tiempo debido a que cada isoacutetopo decae o se transforma en otros siguiendo una serie radioactiva particular
Si observamos cierta cantidad inicial de sustancia o material radioactivo al paso del tiempo se nota un cambio en la cantidad de dicho material la cantidad M del material es una funcioacuten del tiempo esto es M=M(t) al paso del tiempo ocurre una desintegracioacuten o decaimiento del material
Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

Se ha llegado al conocimiento de que en cualquier tiempo tgt0 la rapidez de cambio de la cantidad M(t) de material radioactivo es directamente proporcional a la cantidad y se afirma que
Entonces la solucioacuten general de la ecuacioacuten diferencial es
EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

EJEMPLO Se sabe que un material radioactivo se
desintegra con una rapidez proporcional a la cantidad presente en cualquier instante Si inicialmente hay100mg de material y despueacutes de dos antildeos se observa que el 5 de la masa original se desintegroacute determinar
a) Una expresioacuten para la masa en el momento t
b) El tiempo necesario para que se desintegre el 10 de la masa original
Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

Siacute con y a demaacutes
Expresioacuten para la masa en el momento t-gt
Tiempo necesario para que se desintegre el 10 de la masa original
GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

GRAacuteFICA DE DESINTEGRACIOacuteN
VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

VELOCIDAD DE REACCIOacuteN Cuando se produce una reaccioacuten quiacutemica las
concentraciones de cada uno de los reactivos y productos va variando con el tiempo hasta que se produce el equilibrio quiacutemico en el cual las concentraciones de todas las sustancias permanecen constantes
La velocidad de una reaccioacuten es la derivada de la concentracioacuten de un reactivo o producto con respecto al tiempo tomada siempre como valor positivo
Es decir es el cociente de la variacioacuten de la concentracioacuten de alguacuten reactivo o producto por unidad de tiempo cuando los intervalos de tiempo tienden a 0
EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

EJEMPLO 1 Sea la reaccioacuten
Exprese como varia la concentracioacuten del bromo a lo largo del tiempo
Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

Tiempo (s) [Br2] (moll) Velocidad media
0 00120
38 x 10ndash5
50 00101
34 x 10ndash5
100 00084
26 x 10ndash5
150 00071
24 x 10ndash5
200 00059
EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

EJEMPLO 2
TERMODINAacuteMICA ES LA COMPRESIBILIDAD Una de las cantidades de intereacutes en
termodinaacutemica es la compresibilidad Si una sustancia dada se mantiene a una temperatura constante entonces su volumen V depende de su presioacuten P Podemos considerar la razoacuten de cambio del volumen respecto a la presioacuten a saber la derivada dVdP Conforme P crece V decrece de modo que dVdPlt0
La compresibilidad se define al introducir un signo menos y dividir esta derivada entre el volumen V
compresibilidad isoteacutermica = β = -
En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

En estos teacuterminos β mide queacute tan raacutepido por unidad de volumen decrece el volumen de una sustancia a medida que la presioacuten aumenta a temperatura constante Por ejemplo se encontroacute que el volumen V (en metros cuacutebicos) de una muestra de aire a 25 degC estaacute relacionado con la presioacuten P (en kilo pascales) mediante la ecuacioacuten
V= La razoacuten de cambio de V respecto a P cuando P m 50 kPa
es P=50 = - P=50
= - = - 000212kPa La comprensibilidad a esa presioacuten es
- P=50 = kPa)
USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

USO DE DERIVADAS EN LA FIacuteSICA Sabemos que si y 1048685 f (x) entonces la derivada dydx puede interpretarse como la razoacuten de cambio de y respecto a x En esta seccioacuten se analizan algunas de las aplicaciones de esta idea a la fisica la quiacutemica la biologiacutea la economiacutea y otras ciencias recuerde la idea baacutesica que se encuentra detraacutes de las razones de cambio Si x variacutea de x1 a x2 entonces el cambio en x es 1048685x 1048685 x2 1048685 x1 y el cambio correspondiente en y es 1048685y 1048685 f (x2) 1048685 f (x1) El cociente de diferencias y x f x2 f x1 x2 x1 es la razoacuten de cambio promedio de y respecto a x en el intervalo 1048685x1 x21048685 y puede interpretarse como la pendiente de la recta secante PQ Su liacutemite cuando F(x)x l 0 es la derivada f(x1) la cual puede interpretarse como la razoacuten de cambio instantaacutenea de y respecto a x o sea la pendiente de la recta tangente en P(x1 f (x1)) Si se usa la notacioacuten de Leibniz escribimos el proceso en la forma dy dx liacutem xl0 y x Siempre que la funcioacuten y = f (x) tenga una interpretacioacuten especiacutefica en una de las ciencias su derivada tendraacute una interpretacioacuten especiacutefica como razoacuten de cambio
FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

FIacuteSICA Si s = (t) es la funcioacuten posicioacuten de una partiacutecula
que se mueve en una liacutenea recta entonces Alfa(s)alfa(t) representa el promedio de la
velocidad en un periodo alfa(t) y v = dsdt representa
la velocidad instantaacutenea (la razoacuten de cambio del desplazamiento respecto al
tiempo) La razoacuten de cambio instantaacuteneo de la velocidad respecto al tiempo es la aceleracioacuten
a(t) = vrsquo=(t) = srsquorsquo =(t)
EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

EJEMPLO 3 Si un baloacuten es lanzado verticalmente hacia arriba
con una velocidad de 80 piess entonces su altura despueacutes de t segundos es s=80t-16t^2
A)iquestCuaacutel es la altura maacutexima alcanzada por el baloacuten
B) iquestCuaacutel es la velocidad del baloacuten cuando esta a 96 pies por encima del suelo en su camino en descenso
Primer paso Para resolver el problema del inciso (A) tenemos que saber el segundo en cuando el baloacuten llega a su altura maacutexima sabiendo este dato podemos sustituirlo en la funcioacuten ya esta nos da los pies de altura con el segundo predeterminado
INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

INFORMACIOacuteN Vo= 80 piess = 24384ms tenemos que convertir este dato a
metros para que salgan con las unidades deseadas ya que no sale con piess
G=98ms^2 Formula para sacar el tiempo en el que llega a su punto maacuteximo Vf= vo-gt Despejando t en esta formula= 0=24384ms-98ms^2(t) 98ms^2(t)= 24384ms t= 2438498ms^2 t= 248816 segundos ya sacamos el tiempo que se tarda el
baloacuten en llegar hasta arriba ahora solo hay que sustituir S=80t-16t^2 S= 80(2488)-16(2488)^2 S=19904-9904 S= 100 pies de altura esta es la respuesta del inciso A ya que
esta es la altura maacutexima
Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

Para sacar el inciso (B) tenemos que sacar el segundo en el que el baloacuten esta a 96 pies de altura teniendo este dato le sacamos la derivada a nuestra funcioacuten sacaacutendole la derivada solo hay que sustituir en t el segundo en el que el baloacuten esta a 96 pies de altura
B) S= 80t-16t^2 S=80(2)-16(2)^2 S= 160-64 S= 96 pies de altura Esto significa que cuando el baloacuten recorre el segundo 2 este baloacuten estaraacute a
96 pies de altura entonces con ldquo2rdquo es el numero con el que sustituiremos en la derivada para sacar la velocidad
S=80t-16t^2 Srsquo=80-32t Srsquo=80-32(2) Srsquo=80-64 Srsquo=16 piessegundo (cabe aclarar que esta es la velocidad cuando va en su
camino ascendente ya que es positivo el segundo)
Srsquo=80-32(-2) Srsquo=80+64 Srsquo=144 piessegundo(esta es su velocidad cuando va en descenso)
CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

CONCLUSIOacuteN Como observamos podemos ver que las
matemaacuteticas estaacuten presentes en cualquier cosa que hagas y estaacuten involucradas en todo tipo de aacutereas nosotros nos enfocamos en la quiacutemica fiacutesica y biologiacutea donde observamos el uso de la derivada en estas aacutereas ya sea en encontrar la velocidad el tiempo la distancia y las temperaturas
Estas son algunas de las muchas cosas que se utilizan en estas aacutereas y las derivadas se ven Auacuten maacutes en la quiacutemica han sido fundamentales para poder expresar y calcular mediante ellas razones de cambio que despueacutes se pueden demostrar mediante la praacutectica
Con esto podemos deducir que las matemaacuteticas son fundamentales para todas estas aacutereas y que sin ella no se podriacutean explicar tantas cosas
FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-

FUENTES httpwwwmatusonmx~jldiaz
DocumentsDerivadasrazon20de20cambio-cbpdf
httpfresnopnticmeces~fgutie6quimica2ArchivosHTMLTeo_3_princhtm
Lurcell Varberg Rigdon Calculo Prentice Hall Octava Edicioacuten
Galvaacuten Cienfuegos Elizondo Fabela Rodrigez RomeroCaacutelculo Diferencial para administracioacuten y ciencias Sociales Pearson Educacioacuten2006Meacutexico Segunda Edicioacuten
- Aplicacioacuten de funciones
- Uso de derivadas en quiacutemica
- Introduccioacuten a las funciones
- Slide 4
- 1- FUNCION SOBRE PUNTO DE EBULLICION
- Slide 6
- 2- FUNCIOacuteN SOBRE CRECIMIENTO DE UNA PLANTA
- Slide 8
- Slide 9
- 3- FUNCION SOBRE VARIACION DE TEMPERATURA
- Sustancias radioactivas
- Slide 12
- ejemplo
- Graacutefica de desintegracioacuten
- Velocidad de reaccioacuten
- Ejemplo 1
- Slide 18
- Ejemplo 2 TERMODINAacuteMICA ES LA COMPRESIBILIDAD
- Slide 20
- Uso de derivadas en la fiacutesica
- Fiacutesica
- Ejemplo 3
- Informacioacuten
- Slide 25
- Conclusioacuten
- fuentes
-



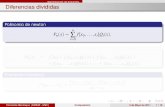








![REPREsENTACIONES INTEGRALES DE LAS FUNCIONES ......DE BESSEL-CLIFFORDDElERCERORDEN Las funciones C (x) de Bessel-Clifford de tercer orden fuer on m,n introducidas por N. Hayek en [6].](https://static.fdocumento.com/doc/165x107/60c26a4fdebbd223cf28b86b/representaciones-integrales-de-las-funciones-de-bessel-clifforddelercerorden.jpg)