ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES … · función f x x x( ) 6 0 2 atraviesa al...
Transcript of ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES … · función f x x x( ) 6 0 2 atraviesa al...

UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
ESCUELA NACIONAL COLEGIO DE CIENCIAS Y HUMANIDADES PLANTEL NAUCALPAN
GUÍA DE MATEMÁTICAS IV PLAN ACTUALIZADO
SEMINARIO LOCAL DE MATEMÁTICAS, TURNO MATUTINO
Naucalpan de Juárez, 2019
Guía de Matemáticas IV.

La presente guía fue elaborada en el Área de Matemáticas del Plantel Naucalpan del Colegio de Ciencias y Humanidades, de la Universidad Nacional Autónoma de México. La publicación es un producto del Seminario Local de Matemáticas del CCH-Naucalpan. Turno Matutino.
Coordinador Ismael Nolasco Martínez
Autores
Angélica Garcilazo Galnares
Blanca Elizabeth Cruz Estrada
Brenda del Carmen Muñoz Ramírez
Dante Octavio Carretero
Emelia Norma Venegas Ocampo
H. Laura Paz Santiago
Ismael Nolasco Martínez
Miriam Sandoval León
Omar Anguiano Sánchez
Pedro Cázares Mena
Sandra Verónica Roldán Meneses
Verónica Méndez Nolasco
Primera versión: Marzo de 2019. D.R. UNAM. CCH. Naucalpan, 2019. Av. De los Remedios No.10 Naucalpan de Juárez. Teléfonos: 53600323; 53600324. Naucalpan de Juárez, estado de México

2
INDICE Pág. FUNCIONES POLINOMIALES Funcion...................................................................................................................................4 Funciones polinomiales..........................................................................................................5 Obtención de ceros.................................................................................................................9 División de polinomios..........................................................................................................14 División sintetica...................................................................................................................15 Factorización directa.............................................................................................................17 Bosquejo de la grafica...........................................................................................................23 Comportamiento de las funciones polinomiales....................................................................25 FUNCIONES RACIONALES Y CON RADICALES
Función racional y con radicales...........................................................................................29 Tipos de funciones racionales...............................................................................................31 Funciones con radicales.......................................................................................................42 FUNCIONES LOGARITMICAS Y EXPONENCIALES
Funciones exponenciales......................................................................................................48 Situaciones que involucran crecimiento y decrecimiento exponencial.................................49 Grafica de la función exponencial.........................................................................................56 Funciones logarítmicas.........................................................................................................64 Ecuaciones exponenciales....................................................................................................77 Logaritmos............................................................................................................................84 Propiedades de los logaritmos..............................................................................................86 Logaritmo natural..................................................................................................................92 Ecuaciones logarítmicas.......................................................................................................96 FUNCIONES TRIGONOMETRICAS
Funciones trigonométricas..................................................................................................107 Ángulos especiales.............................................................................................................109 Graficas de las funciones trigonométricas..........................................................................112 BIBLIOGRAFIA..................................................................................................................124

3
UNIDAD 1. FUNCIONES POLINOMIALES Propósito:
Al finalizar la unidad el alumno habrá avanzado en el estudio de las funciones al introducir la notación funcional y la noción de dominio y rango, relacionando la expresión algebraica de una función polinomial con su gráfica y analizará su comportamiento. Con base en la resolución de problemas y en contexto, usará las gráficas, tablas, expresión matemática para explicar los procesos involucrados. APRENDIZAJES Con relación a los conocimientos y destrezas, el alumno en función de la resolución de problemas:
- Explorará diferentes relaciones, reconociendo las condiciones necesarias para determinar si una relación es función, la simbolizará y distinguirá el dominio y el rango.
- Comprende el significado de la notación funcional, la utilizará para representar y evaluar funciones polinomiales. Usará la notación de intervalos para representar dominio y rango de una función
- Aplicará la división sintética, el teorema del residuo, el teorema del factor, su recíproco para determinar los ceros de f(x) y su gráfica.
- Construirá una función polinomial a partir de las raíces de su ecuación y bosquejará su gráfica y a partir de una función polinomial calculará los ceros y realizará su gráfica.
- Reconocerá a las funciones como modelos de variación de fenómenos naturales, econó-micos y sociales.

4
UNIDAD 1. FUNCIONES POLINOMIALES
DEFINICIÓN DE FUNCIÓN
Una función es una regla de correspondencia entre dos conjuntos, en la cual todo elemento
de un conjunto D (dominio) está asociado con uno y sólo un elemento de otro conjunto C
(contradominio). Al conjunto formado por los primeros elementos de las parejas se le llama
dominio y al conjunto de los segundos elementos de las parejas se le denomina
contradominio. Y para establecer la asociación entre los elementos del dominio con los
elementos del contradominio se emplea una regla de correspondencia. A los valores
obtenidos para la variable dependiente se les conoce como rango de la función.
Ejemplo
Dominio = {Cecilia, Miguel, Joel, Francisco, Verónica, Alejandro, Jazmín, Norma, Juan,
Fabiola}
Regla de Correspondencia =” calificaciones del primer mes en Matemáticas”
Rango = 6, 5, 7, 8, 4, 9, 6, 7.5, 3, 6
Notación de funciones
Para denotar una función se emplea la siguiente notación:
:f A B (se lee como “función de A en B)
A y B por lo general son conjuntos de números reales y la regla de correspondencia se
establecerá por medio de una expresión algebraica y se utilizará la notación:
f(x) (se lee “función de x”) en donde x es un elemento del dominio.
Por ejemplo, al considerar la regla de correspondencia ( ) 2f x x al sustituir un valor
del dominio se obtiene un valor comprendido en el contradominio. Si en la expresión
anterior se considera x = 5; entonces, f (5) = 5 - 2 = 3; por lo tanto, se obtiene la pareja
(5,3).

5
FUNCIONES POLINOMIALES
Una función polinomial es una función de la forma:
1
1 1 0( ) ...n n
n nf x a x a x a x a
Donde 1 1 0, .... ,n na a a a son números reales y n es un entero no negativo. El dominio lo
constituyen todos los números reales. El grado de una función polinomial es el grado del
polinomio en una variable.
Por ejemplo, determina cuál de las funciones siguientes son polinomiales.
4) ( ) 2 3
) ( )
) ( ) 0
) ( ) 8
a f x x
b g x x
c f x
d g x
Solución
a) f es una función polinomial de grado cuatro
b) g no es una función polinomial. La variable x estas elevada a la potencia 1
2que no es un
entero no negativo
c) f es la función polinomial cero; no se le asigna grado alguno
d) g es una función constante diferente de cero, una funcional polinomial de grado cero.

6
TIPOS DE FUNCIONES POLINOMIALES.
Funciones de la forma 0( )f x a función constante
Ejemplo ( ) 4f x Dominio: (-∞,∞) Rango: {4}
Solución:
Para construir la gráfica se obtiene una tabla de valores:
x -1 0 1
f(x) 4 4 4
Función de la forma 1 0( )f x a x a funcion lineal
Ejemplo. ( ) 2 3f x x Dominio: (-∞,∞) Rango (-∞,∞)
Solución:
x -1 0 1
f(x) f(-1)=2(-1)+3=1 f(0)=2(0)+3=3 f(1)=2(1)+3=5

7
Función de la forma 2
2 1 0( )f x a x a x a función cuadrática
Ejemplo 2( ) 2 8 5f x x x Dominio: R Rango: (-∞, 3)
Solución:
X -1 0 1
f(x) f(-1)=-15 f(0)=-5 f(1)=1
Al trazar en la gráfica anterior la recta vertical x = 2, se observa que la curva es simétrica
respecto a esta recta, que recibe el nombre de “eje de simetría”.
Funciones Polinomiales de grado 3 y 4
Las representaciones gráficas de estas funciones están determinadas de acuerdo con el
signo del coeficiente del término de mayor exponente y si el exponente es par o impar.
Caso 1: El coeficiente es positivo y el exponente es impar. Como ejemplo, a continuación,
se muestra la gráfica de la función y = x3

8
Caso 2: El coeficiente es negativo y el exponente es impar. Como ejemplo, a continuación,
se muestra la gráfica de la función 3( ) 2f x x
Caso 3: El coeficiente es positivo y el exponente es par. Como ejemplo, a continuación, se
muestra la gráfica de la función 4( ) 3f x x

9
Métodos de exploración para la obtención de los ceros, aplicables a las funciones
polinomiales factorizables de grado 2 y 4
Por ello, se revisarán algunos conceptos que permitirán determinar la solución o las raíces
de algunas ecuaciones de grado superior a dos.
Una ecuación cuadrática en x tiene la forma: 2 0ax bx c , en donde a ≠ 0; las
constantes a, b y c pertenecen a los números reales.
Resolver una ecuación cuadrática equivale a determinar sus raíces o soluciones y para ello
existen los métodos de factorización, de completar un trinomio cuadrado perfecto y la
aplicación de la fórmula general.
Ejemplo:
Resolver la ecuación de segundo grado: 2 6 0x x
Solución:
Si se pueden determinar dos números que, al multiplicarlos, se obtenga el término
independiente (-6) y la suma de ellos, resulte el coeficiente del término lineal (+1),
entonces la expresión:
2 6 0x x
Es factorizable como ( 3)( 2) 0x x
Al aplicar la propiedad del producto nulo o del factor cero, se obtiene:
( 3) 0
3 0
x
x
( 2) 0
2 0
x
x
Las raíces o soluciones son: 1 23 2x x

10
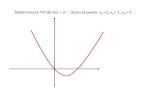
Como las soluciones de la ecuación 2 6 0x x son números reales, la gráfica de la
función 2( ) 6 0f x x x atraviesa al eje de las abscisas en los puntos con
coordenadas (-3 , 0) y (2 , 0) .
Es importante recordar que si la gráfica de una función cuadrática corta al eje de las
abscisas entonces la ecuación cuadrática que le corresponde a dicha función tiene solución
en los reales.
Los ceros de una función son las abscisas de los puntos en donde su gráfica corta el eje de
las x o es tangente a él; así un cero de una función es un valor de la variable para el cual la
función tiene un valor de cero.
Cuando una ecuación cuadrática presenta dificultades para ser factorizada, entonces se
aplica la fórmula general, cuya expresión matemática es la siguiente:
2
1,2
4
2
b b acx
a
A la expresión que se encuentra dentro del radical se le denomina discriminante:
Discriminante = b2 - 4ac

11
El análisis del discriminante proporciona información de las raíces o soluciones de la
ecuación cuadrática como:
Discriminante Raíces o Soluciones Eje de las Abscisas (eje x)
2 4 0b ac 2 reales y diferentes Lo corta en dos puntos
2 4 0b ac 2 reales e iguales Es tangente en un punto
2 4 0b ac 2 complejas y conjugadas No lo corta en ningún punto
Ejemplo:
Dada la función 2( ) 4 3f x x x , determina la solución de la ecuación cuadrática a
partir de la gráfica.
Solución:
Al construir la gráfica de la función 2( ) 4 3f x x x se obtendrá un trazo similar al
siguiente.
En la gráfica se observa que los puntos en que la parábola corta al eje de las abscisas son:
1 21 3x x

12
Ejercicios
Elabora la gráfica de cada función y determina la solución de la ecuación correspondiente
en los casos siguientes:
2 2 2) ( ) 6 9 ) ( ) 5 ) ( ) 3 10a f x x x b f x x x c f x x x
Solución: 3x 1 20 5x x 1 25 2x x
2 2 2) ( ) 2 5 3 ) ( ) 2 6 ) ( ) 3d f x x x e f x x x f f x x x
Solución: 1 2
13
2x x 1 2
32
2x x 1 20 3x x
Ecuaciones bicuadráticas
La ecuación 4 22 8 0x x es una ecuación de grado cuatro, sin embargo, se puede
transformar y expresar en forma de ecuación cuadrática al sustituir x2 por y
Si 2x y , entonces
4 2x y . Por lo tanto, la ecuación4 22 8 0x x
Se expresa en la forma 2 2 8 0y y
Esta es una ecuación cuadrática que, como se ha visto, se puede factorizar y resolver:
2 2 8 0
( 4)( 2) 0
y y
y y
Al aplicar la propiedad del producto nulo se obtiene:
4 0 2 0
4 2
y y
y y
Pero, como y = x2 entonces: x2= 4 x2 = –2
Al determinar la raíz cuadrada en ambos miembros de cada ecuación, se obtiene:
2 2x x i

13
En consecuencia, las cuatro soluciones o raíces de la ecuación cuartica o bicuadrática son:
1 2 3 42 2 2 2x x x i x i
En la figura siguiente se representa la gráfica de la función 4 2( ) 2 8f x x x
Ejercicios
Determina las raíces de las siguientes ecuaciones a partir de los criterios de solución
expuestos en esta sección:
4 2 4 2 4 2
1 2 3 4 1 2 3 4 1 2 3 4
4 2 4 2 4 2
1 2 3 4 1 2 3 4 1 2
) 8 15 0 ) 13 36 0 ) 5 4 0
. 3, 3, 5, 5 3, 3, 2, 2 2, 2, 1, 1
) 6 0 ) 17 16 0 ) 5 6 0
. 3, 3, 2 , 2 4, 4, 1, 1 3 ,
a x x b x x c x x
sol x x x x x x x x x x x x
d x x e x x f x x
sol x x x i x i x x x x x i x
3 43 , 2 , 2i x i x i

14
Divisor Dividendo
Residuo
DIVISIÓN DE POLINOMIOS
Algunas ecuaciones de grado superior a dos se pueden factorizar en dos o más factores
que permite reducir la misma hasta obtener expresiones más sencillas de resolver. La
operación que se utiliza para encontrar los factores es la división algebraica y en la cual su
residuo debe ser cero.
Ejemplo:
Dividir el polinomio 23 1x x entre el binomio 2x , y expresar el dividendo en forma
de dos factores (el cociente y el divisor) más el residuo.
Solución:
Cociente
22 3 1x x x
Las operaciones que se realizan son las siguientes:
Los elementos de esta división son: 23 1x x corresponde al dividendo; 2x es el
divisor; 3 5x es el cociente y 9 es el residuo.
23 6 5 10 (3 5)( 2) 9x x x x x
Dividendo = (divisor)(cociente)+residuo

15
Ejercicios
Realiza las siguientes divisiones aplicando la división de polinomios.
3 2 3 2
2 2
3 2 3 2
2 2
)( 3 2) 2 )(3 8 4 3) 3
. 3 8 3 1 0
)(2 2 1) 1 )(2 2 1)( 1)
. 2 3 5 4 2 1 0
a x x x x b x x x x
sol x x residuo x x residuo
c x x x x d x x x x
sol x x residuo x x residuo
DIVISIÓN SINTÉTICA
La división del polinomio 2x3 - x2 - 5x + 7 entre el binomio x - 3 se puede realizar de la
siguiente manera:
1. Se escriben los coeficientes del dividendo y el término independiente del divisor con signo
contrario en el primer renglón de abajo:
Dividendo Divisor
2x3 - x2 - 5x + 7 x - 3
2 -1 5 7 3
1° renglón
2. Se escribe el primer coeficiente en el tercer renglón
2 -1 - 5 7 3 1er renglón
2º renglón
2 3er renglón
3. El primer coeficiente (2) se multiplica por el termino independiente con signo contrario (+3)
y el producto 2 x 3 = 6 se escribe en el segundo renglón, exactamente debajo del segundo
coeficiente (-1) para después sumarlos. La suma se escribe en el tercer renglón
2 -1 - 5 7 3 1er renglón
6 2º renglón
2 5 3er renglón

16
4. Se continúa este proceso repitiendo el paso anterior, es decir, ahora se multiplica ( 5)
por (+3) y el producto 5 x 3 = 15 se escribe en el segundo renglón, exactamente debajo del
tercer coeficiente (-5) para después sumarlos. La suma de 15 + (-5) = 10 se escribe en el
tercer renglón como se muestra a continuación:
2 -1 - 5 7 3 1er renglón
6 15 2º renglón
2 5 10 3er renglón
5. Nuevamente se repite el proceso para obtener los números que se indican en la
tabla siguiente:
2 -1 - 5 7 3 1er renglón
6 15 30 2º renglón
2 5 10 37 3er renglón
6. El resultado obtenido en el tercer renglón es: 2 5 10 son los coeficientes del
cociente, por lo que la solución de la división es: 22 5 10x x
El último número del tercer renglón (37) es el residuo
Ejercicios
Realiza las siguientes divisiones aplicando la división sintética.
3 2 3 2
2 2
3 2 3 2
2 2
3 2 3 2
2 2
)( 3 2) 2 )(3 8 4 3) 3
. 3 8 3 1
)(2 2 1) 1 )(2 2 1) 1
. 2 3 1 2 1
)( 3 2 7 2) 2 )(4 10 5 3) 3
. 3 4 1 4 2 1
a x x x x b x x x x
sol x x residuo x x
c x x x x d x x x x
sol x x x x
e x x x x f x x x x
sol x x x x

17
ECUACIONES CÚBICAS QUE SE RESUELVEN POR FACTORIZACIÓN DIRECTA
La multiplicación de dos o tres binomios da como resultado una ecuación de segundo o de
tercer grado y de n binomios multiplicados se obtiene una ecuación de grado n.
La multiplicación de un binomio ( )x a por otro binomio ( )x b se puede realizar de la
siguiente manera:
Cada uno de los términos del primer binomio ( )x a multiplica al segundo binomio
(x + b):
( )( ) ( ) ( )
( )( ) ( ) ( ) ( ) ( )
x a x b x x b a x b
x a x b x x x b a x a b
Es igual escribir ( )a x que ( )x a , por lo que se ordenan los términos:
2
( )( ) ( ) ( ) ( ) ( )
( )( )
x a x b x x x b x a a b
x a x b x bx ax ab
El producto ab equivale a multiplicar los términos que no contienen a la literal x de los
binomios que se están multiplicando ( )( )x a x b .Los términos semejantes se reducen y
se obtiene el producto. 2( )( ) ( )x a x b x b a x ab
Ejemplo
Obtén las raíces de la ecuación: 3 23 4 12 0x x x
Solución:
Esta es una ecuación de tercer grado con todos sus términos y ordenada en forma
decreciente de acuerdo a sus exponentes. Por lo que una forma de obtener las raíces es
proceder a factorizar de manera que los tres factores sean lineales.
En la ecuación el término independiente es - 12.

18
Este número se puede expresar como un producto de factores numéricos como las
siguientes:
a) ( -1 )( 2 )( 6 ) = - 12
b) ( -2 )( 2 )( 3 ) = -12
c) ( 1 )( -3 )( 4 ) = -12
d) ( 1 )( -1 )( -12 ) = -12
Al utilizar los valores del inciso a) ( -1 ) ( 2 ) ( 6 ) se tendría que:
1 2 31 2 6x x x
Esto se realiza expresando la ecuación como una función: 3 2( ) 3 4 12P x x x x y se
sustituye el valor de nx , considerando que si se obtiene que ( ) 0nP x entonces el
binomio ( )nx x es factor, en caso de que ( ) 0nP x entonces el binomio ( )nx x no es
factor.
A continuación, se comprueba si el primer binomio propuesto (x – 1) es o no factor de
3 23 4 12x x x . Si es uno de los factores, entonces x - 1 = 0, por lo tanto, x = 1
3 2( ) 3 4 12P x x x x
3 2(1) (1) 3(1) 4(1) 12P
(1) 1 3 4 12P
(1) 4 16P
(1) 12P
Como (1) 12P , entonces el binomio propuesto 1x no es factor de
3 23 4 12x x x ; por lo que todas las combinaciones que contengan x = 1 no
serán factores. Ahora se selecciona el valor de x = - 2 del inciso b) para determinar si es o
no uno de los factores de 3 23 4 12x x x
3 2( ) 3 4 12P x x x x

19
3 2( 2) ( 2) 3( 2) 4( 2) 12P
( 2) 8 12 8 12P
( 2) 0P Como P( -2 ) = 0, entonces ( x + 2 ) es uno de los factores de 3 23 4 12x x x ,
por lo
Tanto: 3 23 4 12x x x = ( 2)[ ( )]x Q x
Para conocer el valor de Q(x) se divide 3 23 4 12x x x entre 2x por medio de la
división sintética:
1 3 -4 -12 -2 1er renglón
-2 -2 12 2º renglón
1 1 -6 0 3er renglón
Del tercer renglón,
el residuo es cero y el cociente es 2 6x x , así que Q(x) = 2 6x x
Por lo tanto, se puede escribir que:
3 2 23 4 12 ( 2)( 6)x x x x x x
2 6x x se puede factorizar de la siguiente forma: ( 2)( 3)x x
En consecuencia, se tiene que:
3 2 23 4 12 ( 2)( 6)x x x x x x
3 23 4 12 ( 2)( 2)( 3)x x x x x x
de esta manera la ecuación 3 23 4 12 0x x x se expresa como:
( 2)( 2)( 3) 0x x x
Finalmente, utilizando la propiedad del producto nulo se tiene que:
2 0 2
2 0 2
3 0 3
x x
x x
x x
Así, las raíces de la ecuación 1 2 32 2 3x x x

20
Para obtener la gráfica de la función P(x) se elabora una tabla de valores con dos
columnas, en la primera se proponen valores para la variable independiente (x) y en la
segunda se escriben los valores correspondientes de la variable dependiente P(x).
Estos valores se pueden observar en la gráfica siguiente:
Ejercicios
Realiza las operaciones necesarias para encontrar el valor de las raíces o soluciones de las
siguientes ecuaciones cúbicas:
3 2
1 2 3
3
1 2 3
3 2
1 2 3
3 2
1 2 3
3 2
1 2 3
3
1 2 3
) 6 11 6 0 . 3 2 1
) 7 6 0 . 1 3 2
) 4 6 . 3 2 1
) 8 17 10 0 . 1 2 5
) 3 13 15 0 . 1 5 3
) 19 30 0 . 2 5 3
a x x x sol x x x
b x x sol x x x
c x x x sol x x x
d x x x sol x x x
e x x x sol x x x
f x x sol x x x
Se continuará con el mismo procedimiento, pero ahora se consideran ecuaciones de 4º
grado

21
Ejemplo:
Determinar las raíces de la ecuación: 4 3 216 4 48 0x x x x
Solución:
Algunos de las posibles combinaciones de factores numéricos del 48 son:
)(2)(2)(3)(4) )(2)(2)( 3)( 4) )( 2)( 2)(3)(4)
)(1)(4)(3)(4) )(1)(2)(6)(4) )(1)(2)(3)(8)
a b c
d e f
Se selecciona el valor de x = 2 para determinar si es o no uno de los factores de
4 3 216 4 48 0x x x x
Se evalúa x = 2 en la expresión polinomial:
4 3 2
4 3 2
( ) 16 4 48
( ) (2) (2) 16(2) 4(2) 48
( ) 16 8 64 8 48 0
P x x x x x
P x
P x
Como P (2) = 0 entonces x – 2 es un factor:
4 3 216 4 48 ( 2) ( )x x x x x Q x
Por lo que:
4 3 216 4 48( )
2
x x x xQ x
x
Se puede obtener la expresión correspondiente para Q(x) al realizar la operación de
división algebraica para obtener que:
3 2( ) 14 24Q x x x x
Los posibles factores numéricos del -24 son
)(2)(3)( 4) )(2)( 3)(4)a b
Se selecciona el valor de x = -3 para determinar si es o no uno de los factores de
3 2 14 24x x x Se evalúa x = - 3 en la expresión polinomial:

22
3 2( ) 14 24
( 3) ( 3)3 ( 3)2 14( 3) 24
( 3) 27 9 42 24 0
Q x x x x
Q
Q
Como Q(-3) = 0, entonces x + 3 es un factor: 3 2 14 24 ( 3) ( )x x x x R x
Por lo que:
3 2( ) 14 24
3
R x x x x
x
Se puede obtener la expresión correspondiente para R(x) al realizar la operación de
división algebraica anterior para obtener que: 2( ) 2 8R x x x
Sin embargo, R(x) se puede factorizar como: ( ) ( 4)( 2)R x x x
Con estas expresiones para R(x) y Q(x), la ecuación de cuarto grado se puede escribir
como:
4 3 2
4 3 2 3 2
4 3 2
4 3 2 2
4 3 2
16 4 48 ( 2) ( )
16 4 48 ( 2)( 14 24)
16 4 48 ( 2)( 3) ( )
16 4 48 ( 2)( 3)( 2 8)
16 4 48 ( 2)( 3)( 4)( 2)
x x x x x Q x
x x x x x x x x
x x x x x x R x
x x x x x x x x
x x x x x x x x
La ecuación 4 3 216 4 48 0x x x x
Se puede expresar como ( 2)( 3)( 4)( 2) 0x x x x
Al aplicar la propiedad del producto nulo, resulta que:
2 0 2
3 0 3
4 0 4
2 0 2
x x
x x
x x
x x
Así las raíces o ceros de la ecuación 4 3 216 4 48 0x x x x son:
1 2 3 42 3 4 2x x x x

23
En la gráfica de la figura siguiente se muestra que la función corta al eje de las abscisas en
los valores correspondientes a las soluciones o ceros de la misma.
BOSQUEJO DE LA GRÁFICA DE UNA FUNCIÓN POLINOMIAL
A partir de la gráfica de una función polinomial se puede realizar un análisis sobre el
comportamiento de la misma. Si bien algunos de los elementos se han destacado en las
secciones previas, es importante considerarlos nuevamente.
Intersecciones de la gráfica con los ejes cartesianos
Se ha señalado que los puntos en los que una función polinomial se intersecta con el eje de
x; representa los denominados ceros de la función ( ) 0f x y que tales ceros representan
las raíces de la ecuación polinomial que se obtiene al hacer ( ) 0f x . Por ejemplo, si se
tiene la función polinomial 2( ) 2 8f x x x , a partir del trazo de su gráfica se observa
que se intersecta en los puntos x = - 2 y x = 4, como se muestra en la figura siguiente:

24
Al hacer ( ) 0f x se tendrá: 2 2 8x x
Al resolverla, por factorización: 2 2 8 ( 4)( 2) 0x x x x
De donde, se obtiene que x = 4 y x = -2
Si se analiza una función cúbica o una de grado 4, o de grado 5 o de un grado mayor, e
incluso, una lineal se podrá comprobar que los ceros de su gráfica, son puntos de
intersección con el eje de las x, representan las raíces de la ecuación polinomial
correspondiente, que se obtiene cuando la función f(x) es igual a cero, es decir ( ) 0f x
Por ejemplo, la función 0 1( ) ( )f x f x tiene la gráfica siguiente:
Los ceros de la función corresponden a x = 0, x = - 2 y x = 1 que son los valores que
corresponden a las raíces de la ecuación 3 2 2 0x x x

25
ANÁLISIS DEL COMPORTAMIENTO DE LAS FUNCIONES POLINOMIALES
El coeficiente del término de mayor grado de la función es determinante para las
características de la gráfica. Si tal coeficiente, na , es positivo y el exponente o grado es
impar, la gráfica será creciente como se muestra en la siguiente figura.
Gráficas de las funciones: 3 52 3 2 1 2 1y x y x y x
Es decir, una gráfica es creciente cuando para toda 0 1x x se obtiene que:
0 1( ) ( )f x f x
Si el coeficiente, es negativo y el exponente o grado es impar, la gráfica será decreciente
como se muestra en la figura siguiente:
3 5( ) 2 3 ( ) 2 1 ( ) 2 1f x x f x x f x x

26
Es decir, una gráfica es decreciente cuando para toda 0 1x x se obtiene que:
0 1( ) ( )f x f x
Cuando la curva es decreciente y a partir de un punto, llamado punto de inflexión, se
transforma en creciente se dice que la gráfica es cóncava hacia arriba. 2( ) 3f x x función
cóncava hacia arriba
Cuando la curva es creciente y a partir de un punto se transforma en decreciente se dice
que la curva es cóncava hacia abajo.
2( ) 3f x x función cóncava hacia abajo.

27
Si el coeficiente na es mayor que 1 la gráfica de la función tiende a hacerse más angosta;
mientras, que si na es menor que 1 y más cercana a cero se hace más amplia.

28
UNIDAD 2. FUNCIONES RACIONALES Y FUNCIONES CON RADICALES Propósito:
Al finalizar la unidad el alumno modelará algunas situaciones que dan lugar a funciones racionales y con radicales, analizará una gráfica para identificar su dominio, rango, asíntotas y relacionar estas características con la situación problemática planteada. APRENDIZAJES
Con relación a los conocimientos y destrezas, el alumno en función de la resolución de problemas:
- Explorará situaciones que se modelan con funciones racionales
- Identificará los elementos de una función racional: ceros, asíntotas verticales y huecos,
dominio y rango para graficarla.
- Graficará funciones que tengan asíntota horizontal diferente al eje de las x, asíntotas verticales, ceros, huecos, dominio y rango.
- Resolverá problemas de aplicación.
- Explorará problemas sencillos que se modelen con Funciones con Radicales.
- Identificará los elementos de la función: dominio, rango, ceros y traza su gráfica.
- Resolverá problemas de aplicación.

29
FUNCIONES RACIONALES Y CON RADICALES
Una función racional es un cociente de dos funciones polinomiales, con el requisito
adicional de que sólo estará definida en todo número real que no sea una raíz del denominador.
Esto es, una función racional es
g xf x
h x donde ,g x h x son funciones polinomiales
y definida para cualquier x , número real, tal que h x no sea cero.
Una función con radicales será aquella en la que aparezcan raíces de la variable
independiente x. En el caso de las funciones con radicales sólo se tratará el caso2( )f x ax bx c , donde ó a b es distinto de cero y c es cualquier número real.
Su dominio es el conjunto de números reales x tales que 2 0ax bx c .
Comenzaremos estudiando a las funciones racionales.
CASO 1
Forma a
f x cx b
Ejemplo 1
Determina Dominio, rango y gráfica de las siguientes funciones racionales.
1) 1
( )f xx
Lo primero es notar que ya que cuando 𝑥 = 0 tenemos 1
00
f , no es un número real.
Entonces, 𝑥 = 0 no está en el dominio de la función, lo cual se escribe de la siguiente manera:
0 0fD x x
La primera parte se lee “El dominio de f es el conjunto de todos los números reales excepto el 0”. La segunda se lee (el dominio de f) “es el conjunto de todas las x, que pertenecen a los números reales, y que son distintas de cero”.
Puedes elegir la que te parezca más clara.

30
Dando valores a x y elaborando una tabla con los correspondientes valores de f, tendremos:
x 1
f xx
,x y x 1
f xx
,x y
0.1 1
0.1 100.1
f
0.1, 10 0.1 1
0.1 100.1
f 0.1,10
1 1
1 11
f
1, 1
1
11 1
1f
1,1
2 1
2 0.52
f
2, 0.5 2 1
2 0.52
f 2,0.5
3 1
3 0.333...3
f
1
3,3
3 1
3 0.333...3
f 1
3,3
Observa cómo a medida que los valores positivos de x están cerca de cero, los valores
correspondientes de f comienzan a crecer rápidamente, y a la inversa: cuando los valores de x son muy grandes los de f se vuelven muy pequeños. La gráfica tiene este aspecto:
Se puede observar que la gráfica nunca llegará a tocar el eje x.

31
Esto significa que nunca se llega a tener f = 0. En otras palabras, el rango de la función incluye a todos los números reales, excepto al cero, lo cual se escribe así:
0 0fR y y
Cuya primera parte se lee: “El rango de f es el conjunto de todos los números reales excepto el 0”. La segunda parte se lee: (el rango de f) “es el conjunto de todas las y, que pertenecen a los números reales, y que son distintas de cero”.
OBSERVACIÓN
Dada la regla de correspondencia de una función f x , al pasar a una nueva regla
𝑓(𝑥 + 𝑐) se obtendrá un desplazamiento horizontal de la gráfica de la función 𝑓(𝑥) original
(en la dirección negativa si c es positiva, y viceversa); por otra parte, al hacer f x c se
observará un desplazamiento vertical de la gráfica original de 𝑓(𝑥) (en la dirección positiva
si c es positiva, y viceversa).
TIPOS DE FUNCIONES RACIONALES
Ejemplos
Determina dominio, rango y gráfica de las siguientes funciones:
1. 𝑔(𝑥) =1
𝑥+1
Observemos en primer lugar, que si consideramos la función más simple 𝑓(𝑥) =1
𝑥, esta
nueva función 𝑔(𝑥) corresponde a tener 𝑓(𝑥 + 1). Entonces, la gráfica de 𝑔(𝑥) presentará un desplazamiento horizontal de una unidad hacia la izquierda, respecto a la gráfica de
𝑓(𝑥) =1
𝑥; al considerar esto, se ve que la gráfica de 𝑔(𝑥) tendrá este aspecto:
Es posible observar que, como resultado del desplazamiento hacia la izquierda, la gráfica de g se aproxima a la línea x = -1 en lugar de hacerlo al eje y. La línea x = -1 es una asíntota: una línea a la cual la gráfica se aproxima cada vez más, pero sin llegar a tocarla.

32
x = -1 es una asíntota vertical; se puede ver que también hay una asíntota horizontal: para valores grandes de x, la gráfica se va acercando cada vez más al eje x pero sin llegar a tocarlo nunca. Entonces la línea y = 0 es dicha asíntota horizontal.
La gráfica misma nos permite ver que el dominio y el rango de g son
𝐷𝑔 = {𝑥 ∈ ℝ|𝑥 + 1 ≠ 0} = {𝑥 ∈ ℝ|𝑥 = −1}
𝑅𝑔 = ℝ − {0}
2. 3
2 3f x
x
En esta ocasión, debemos observar que la función no estará definida si ocurre que
2𝑥 − 3 = 0. Esto significa que el dominio será
2 3 0fD x x
Es decir, “el conjunto de todos los valores x que sean números reales, tales que 2x – 3 sea distinto de cero”.
Tomando la expresión 2𝑥 − 3 = 0 y resolviendo para 𝑥, se tiene que 𝑥 =3
2. Entonces el
dominio también se puede escribir como
32fD x x
Es decir, “el conjunto de todos los valores x que sean números reales, tales que x sea
distinto de 3
2”.
De paso, la línea 𝑥 =3
2 será una asíntota vertical: la gráfica se irá acercando cada vez más
a ella, pero nunca la tocará.
Esta asíntota vertical divide el dominio de la función en dos regiones; de un modo similar a lo que se hacía con funciones polinomiales, podemos analizar el comportamiento de esta función en cada una de dichas regiones:
Para 𝑥 <3
2, tomemos x = 1. Entonces la función queda 𝑔(2) =
1
2(1)−3=
1
−1= −1, lo que
significa que en esta región, la gráfica quedará por debajo del eje x.
Para 𝑥 >3
2, tomemos x = 2. La función queda 𝑔(0) =
1
2(2)+1=
1
1= 1. Esto quiere decir que
en esa región, la gráfica quedará por encima del eje x.
Para determinar la asíntota horizontal, podemos analizar lo que ocurre con esta función cuando x va tomando valores cada vez mayores:

33
Si x se vuelve muy grande, la operación 3
2𝑥−3 dará valores cada vez más pequeños
(verifícalo usando una calculadora). Es decir, f(x) se aproximará a cero conforme x se vuelve grande. Sin embargo, nunca llegará a valer exactamente cero. Entonces, la línea f = 0 es la asíntota horizontal de esta función, y el rango será
0fR
La gráfica es la siguiente:
3. 1
( )3
f xx
Encontrando las asíntotas (vertical y horizontal) y determinando el comportamiento de la gráfica en las regiones en que queda dividido el dominio por efecto de la asíntota
horizontal, podemos ver que 3 0 3fD x x x x , y que la gráfica será:

34
4. 1
( ) 22 1
f xx
Los argumentos empleados en los ejemplos anteriores permiten notar que, respecto a la
gráfica de 𝑓(𝑥) =1
𝑥, ésta tendrá un desplazamiento horizontal (de −
1
2 unidad) y luego uno
vertical (de 2 unidades):
1
2 1 02
fD x x x x
El rango es 2 2fR y y

35
5. 1
32
f xx
Usa los argumentos anteriores para comprender porque el dominio es:
2 0 2fD x x x x
Y la gráfica tiene este aspecto:
El rango es 3fR
6. 6 5
( )2 3
xf x
x
Como la función no está definida en 2𝑥 − 3 = 0, tenemos una asíntota vertical en 𝑥 =3
2, y
de paso el dominio de la función es3
2fD
.
Para hallar la asíntota horizontal, exploramos el comportamiento de la función para valores muy grandes de x:

36
Analicemos por separado numerador y denominador.
En el caso del numerador 6𝑥 − 5, al volverse x muy grande, -5 se vuelve una cantidad
insignificante frente a 6x, de modo que 6𝑥 − 5 se aproximará a 6x.
En el caso del denominador 2𝑥 − 3, conforme x se vuelve grande, -3 se hace despreciable frente a 2x, por lo que el denominador se irá aproximando a 2x.
Entonces, cuando x toma valores muy grandes, 𝑓(𝑥) =6𝑥−5
2𝑥−3 se aproxima a la expresión
6𝑥
2𝑥=
6
2= 3.
Esto significa que 𝑓 = 3 es la asíntota horizontal para esta función.
La gráfica tendrá este aspecto:
El rango es 3fR .
CASO 2
2
( )a
f x cx b
Tomemos como patrón 2
1f x
x , esto es hacer 1, 0a b c en
2
( )a
f x cx b
.
Las ideas principales siguen siendo las mismas: la función no está definida si 𝑥2 = 0, y
cuando x se vuelve grande, la operación 1
𝑥2 se vuelve cada vez más cercana a cero. Esto
significa que 0fD .
En esta ocasión, sin embargo, ( )f x siempre será positiva (debido a que al elevar al
cuadrado un número real, el resultado es siempre positivo). Esto implica que
0fR y y .

37
Ejemplo
2
11) ( )
1f x
x
Esta gráfica presentará un desplazamiento horizontal de -1 unidades respecto a la de
𝑔(𝑥) =1
𝑥2. Así, tendrá este aspecto:
El rango y el dominio serán 1 1fD x x , 0fR y y .

38
2
22)
3 1f x
x
Vemos que 1
3 1 03
fD x x x x
. Además, f sigue siendo siempre positiva.
La gráfica es:
El rango por su parte es fR .
2
13) 1
2 3f x
x
1.5fD . La gráfica:
1fR y y

39
24)
1
xf x
x
En esta ocasión, la función no estará definida cuando 𝑥2 − 1 = 0, lo cual tiene dos
soluciones: 𝑥 = 1 y 𝑥 = −1. Esto significa que 1,1fD .
Además podemos hallar el punto donde la gráfica corta al eje x, si escribimos
𝑥
𝑥2 − 1= 0
La solución es simplemente x = 0.
Los puntos 𝑥 = 1, 𝑥 = 0 y 𝑥 = −1 dividen el dominio en cuatro regiones; analizando el comportamiento de la gráfica en cada una de ellas tendremos lo siguiente:
) Si 1i x , tomemos 2x . Entonces tendremos
2
2 22
32 1f
. Esto quiere
decir que la gráfica estará por debajo del eje x en esta región.
) Si 1 0ii x , tomemos 1
2x . Entonces
2
1 1 11 22 2 2
1 32 31 114 42
f
, lo que
significa que la gráfica estará por encima del eje x.
) Si 0 1iii x , por ejemplo 1
2x , se tendrá
2
1 1 11 22 2 2
1 32 31 114 42
f
, de manera
que la gráfica estará por debajo del eje x en esta región.
) Si 1iv x , hagamos 2x . Entonces
2
2 22
32 1f
. Con esto vemos que la gráfica
estará por encima del eje x cuando x >1.

40
Reuniendo toda esta información, la gráfica de la función será:
fR
5)
2
2
2 3( )
4
x xf x
x
Los mismos argumentos del ejemplo anterior permiten notar que el dominio es
2,2 , 2 ( 2,2) (2, )fD
Al explorar el comportamiento de la función conforme x se vuelve muy grande (para determinar la asíntota horizontal), notaremos lo siguiente:
Numerador. Conforme x crece, llegará un momento en el que tanto -3 como 2x se volverán
muy pequeños comparados con 𝑥2. Así que llegado ese momento, el numerador se
aproximará a 𝑥2.
Denominador. Conforme x crece, muy pronto se ve que -4 se vuelve despreciable frente a
𝑥2. Entonces, cuando x toma valores grandes, el denominador se aproxima a 𝑥2.
De lo anterior, resulta que cuando x es muy grande, la función 𝑓(𝑥) =𝑥2+2𝑥−3
𝑥2−4 se aproxima
a 𝑓(𝑥) =𝑥2
𝑥2= 1. Así que 𝑓 = 1 es la asíntota horizontal de esta función.

41
Al igualar 𝑥2+2𝑥−3
𝑥2−4= 0 se encuentran las intersecciones de la gráfica con el eje x. Se puede
verificar fácilmente que las soluciones son 3, 1x x .
Reuniendo toda esta información, la gráfica resulta tener este aspecto:
fR

42
FUNCIONES CON RADICALES
Una función con radicales, como su nombre lo indica, es aquella que presenta raíces de la variable independiente x.
A continuación se presentan algunos ejemplos relativos a las funciones con radicales. Léelos con cuidado para que apliques lo aprendido en la serie de ejercicios.
Ejemplo.
Determina dominio, rango y gráfica de las siguientes funciones:
1) f x x
Como en la función aparece la operación raíz cuadrada, y esa operación sólo está definida
cuando el radicando es positivo, resulta que el dominio es 0fD x x .
Debido a una restricción con la definición de función (en la que no ahondaremos), sólo
podemos tomar en cuenta el signo positivo de √𝑥. Tomando unos cuantos valores de x para calcular los correspondientes valores de f, se encuentra que la gráfica tiene este aspecto:
El rango resulta ser 0fR y y .

43
2) 3f x x
Los argumentos del ejemplo pasado llevan a concluir que el dominio es
3 0 3fD x x x x
La gráfica:
Y el rango:
0fR y y
3) ( ) 2 3f x x
En esta ocasión, 2
2 3 03
fD x x x x
. Así que la gráfica queda:
Se puede ver que el rango es
0fR y y .

44
4) ( ) 1 2f x x
El radicando, −1 − 𝑥, debe ser positivo para que la función esté definida. Esto nos lleva a
concluir que el dominio es 1 0 1fD x x x x .
Además, el 2 que aparece restando fuera de la raíz desplazará la gráfica dos unidades hacia abajo. Así, la gráfica queda:
El rango resulta ser
2fR y y .
5) ( ) 1f x x
Esta vez el dominio es 0 0fD x x x x ; el 1 que aparece sumando fuera
de la raíz mueve la gráfica una unidad hacia arriba; pero además el signo negativo de la raíz indica que debemos tomar en cuenta sólo sus valores negativos. Esto hace que la gráfica sea como se ve a continuación:

45
Así, el rango es
1fR y y .
26) 4f x x
El hecho de que 𝑥2 − 4 deba ser positivo nos lleva a descubrir que x debe cumplir una de dos condiciones: o bien 𝑥 ≤ −2, o bien 𝑥 ≥ 2. Entonces el dominio es
2 4 0 2 ó 2fD x x x x x
Y la gráfica tiene este aspecto:
Se aprecia que el rango es
0fR y y .
27) 9f x x
Al requerir que 9 − 𝑥2 sea positivo, se encuentra que x debe cumplir con la condición
−3 ≤ 𝑥 ≤ 3. Esto implica que el dominio es 29 0 3 3 fD x x x x .La
gráfica tendrá el aspecto que se muestra:
Por otro lado, se ve que el rango es 0 3 fR y y .

46
Serie de ejercicios
Determina Dominio, rango y Gráfica de:
11) ( )
3f x
x
2
111) ( )
4
xf x
x
21) ( ) 2 5f x x
12) ( )
2 5f x
x
2
212) ( )
2f x
x
22) ( ) 3 4f x x
23) ( )
5 5f x
x
2
213) ( )
4 1f x
x
23) ( ) 1f x x
24) ( )
5f x
x
2
114) ( )
1f x
x
24) ( ) 2 1 2f x x
35) ( )
4 5f x
x
2
115) ( ) 2
1f x
x
25) ( ) 1f x x
16) ( ) 4
4f x
x
2
116) ( ) 3
2f x
x
226) ( ) 4f x x
17) ( ) 2
3 1f x
x
2
2
3 117) ( )
4
xf x
x
227) ( ) 9f x x
6 18) ( )
3 4
xf x
x
1
18) ( ) 1f xx
228) ( ) 4 2f x x
19) ( )
2 3
xf x
x
2
2
119) ( )
2 9
xf x
x
229) ( ) 9 2f x x
110) ( )
xf x
x
2
220) ( ) 3f x
x
230) ( ) 6f x x

47
UNIDAD 3. FUNCIONES LOGARITMICAS Y EXPONENCIALES
Propósito:
Al finalizar la unidad el alumno utilizará las funciones exponencial y logarítmica para representar formas de variación de fenómenos de la naturaleza, que éstas permitan modelar. Retomará los conceptos de dominio y rango, así como el análisis de las relaciones entre los parámetros de estas funciones y su gráfica. APRENDIZAJES Con relación a los conocimientos y destrezas, el alumno en función de la resolución de problemas:
- Explorará situaciones o fenómenos que corresponden a crecimiento o decaimiento ex-ponencial, las relaciones o condiciones existentes y analizará las formas de variación.
- Identificará patrones de cambio involucrados en el crecimiento o decrecimiento de una función exponencial y bosquejará su gráfica.
- Identificará el dominio y rango de una función exponencial y trazará su gráfica.
- Analizará la relación entre las gráficas de funciones exponenciales con diferentes bases incluyendo el número e
- Resolverá problemas en diferentes contextos, que se modelen con funciones exponen-ciales.
- Verificará mediante gráficas o tablas que la función logarítmica es la función inversa de la exponencial. Expresará verbalmente las relaciones: bY=x ↔ y=logb x
- Graficará funciones logarítmicas e identificará su dominio y rango..
- Operará con logaritmos de distintas bases y aplicará sus propiedades.
- Resolverá problemas en diferentes contextos que se modelen con funciones logarítmicas y exponenciales.
- Resolverá problemas de aplicación empleando los conocimientos adquiridos anteriormente.

48
FUNCIONES EXPONENCIALES
La función exponencial es de gran importancia en Matemáticas, es llamada también función
de crecimiento y es utilizada en diferentes áreas de conocimiento pues representa
fenómenos como crecimiento animal, vegetal, económico, epidemias, entre otras. En el
crecimiento exponencial, cada valor de y se obtiene multiplicando el valor anterior por una
cantidad constante a .
La función exponencial sirve para describir cualquier proceso que evolucione de modo que
el aumento (o disminución) en un pequeño intervalo de tiempo sea proporcional a lo que
había al comienzo del mismo.
La función exponencial se representa por medio de la siguiente expresión algebraica:
, 0, 1.xy a a a
A la gráfica de esta función, se le llama curva exponencial. Observa que en este tipo de
funciones, la variable es un exponente. Si la base , se trata de un decrecimiento
exponencial.
Cuando la base es el llamado número Neperiano e , representa a la función exponencial
natural y aparece de la forma:
0; 0.kxy ce c k
Donde ...71828.2e ; a este número también se le llama Número de Euler (en honor del
gran matemático Francés Leonard Euler), c es el valor inicial (para x=0), x es el tiempo
transcurrido k es el factor por el que se multiplica en cada unidad de tiempo.

49
SITUACIONES QUE INVOLUCRAN CRECIMIENTO Y DECRECIMIENTO
EXPONENCIAL.
Algunas de las aplicaciones de la función exponencial son las siguientes:
• Crecimiento de poblaciones.
• Interés de dinero acumulado.
• Desintegración radioactiva.
Se describe brevemente la definición de la función exponencial para estas aplicaciones:
Interés compuesto.
En el interés compuesto los intereses producidos por un capital inicial se van
acumulando durante un tiempo , para producir nuevos intereses. Los intervalos de tiempo,
al cabo de los cuales los intereses se acumulan al capital, se llaman periodos de
capitalización o de acumulación. Si son es el tiempo y es el interés anual en %; el
capital final obtenido se obtiene de la siguiente forma:
Crecimiento de poblaciones.
Dada una población (de personas, bacterias u otra especie viviente) que con el tiempo
tiende a crecer proporcionalmente de acuerdo a la cantidad existente (considerando que la
tasa de mortalidad, nacimientos, no sufren cambios abruptos muy grandes como guerras,
0( ) 1
ntr
C t Cn
Para n incrementos por año; (n mensual, semestral, bimestral, etc.).
Para crecimiento continuo.
0( ) r tC t C e

50
epidemias, etc.), estos modelos de crecimiento pueden cuantificarse a futuro, mediante la
función de crecimiento exponencial que está dada por:
Desintegración radiactiva.
Determinadas sustancias radioactivas decrecen en forma exponencial. En tales casos, si a
es la base de un modelo exponencial de decaimiento, entonces 0 1a .Un ejemplo de
este tipo, es la desintegración de una sustancia radiactiva o isótopo. Las sustancias
radiactivas se desintegran con el paso del tiempo. La cantidad de una cierta sustancia que
va quedando a lo largo del tiempo está dada por:
0 0( ) ; .
.
( ) .
.
ktP t P e P Población inicial
t tiempo
P t Población en el tiempo t
k Tasa de crecimiento relativa
0
0
0
( ) ; 0 1
.
.
( ) .
:
( ) .
t
kt
M t M a a
M Masa inicial
t tiempo
M t Masa que queda en el tiempo t
También se puede expresar como
M t M e k es la tasa de decrecimiento relativo
Un concepto muy utilizado en la desintegración radioactiva es el de vida media o periodo
radiactivo de un isótopo, que es el tiempo requerido para que la mitad de la cantidad
original de una muestra se desintegre.

51
Ejemplo
Un padre deja a su hijo como herencia una hectárea de tierra, el hijo, hombre trabajador,
trabaja durante 10 años el patrimonio heredado un 10% anual de manera constante. ¿Con
que superficie hace crecer durante ese tiempo el hijo al final de los 10 años?
Al término del primer año el hijo tendrá de extensión de tierra:
1 11 (1) 1 1.1 .
10 10hectáreas
Al término del segundo año el hijo tendrá de extensión de tierra:
21 1 1 1 11 1 1 1 (1.1)
10 10 10 10 10hectáreas
Al término del tercer año el hijo tendrá de extensión de tierra:
2 2 2 3
31 1 1 1 1 11 1 1 1 1 (1.1)
10 10 10 10 10 10hectáreas
.
Siguiendo con este razonamiento se tiene que al término del décimo año el hijo terminará
con una extensión de tierra dada por la expresión:
10
1011 (1.1) 2.57
10hectáreas
Ejemplo
Un empresario hace una inversión de 1 millón de pesos que gana el 5% de interés anual
compuesto.
¿Cuál es la cantidad a retirar en 20 años?
Puesto que:
5 15%
100 20
la cantidad que puede retirarse al término del primer año es:
1 11 (1) 1 1.05 .
20 20millones de pesos
Al término del segundo año, el inversionista retiraría:

52
2
21 1 1 1 1 11 1 1 1 1 1.05 .
20 20 20 20 20 20millones de pesos
Al término del tercer año, el inversionista retiraría:
2 2 2
31 1 1 1 11 1 1 1 1.05 .
20 20 20 20 20millones de pesos
Siguiendo este razonamiento, al término del vigésimo año retiraría:
20201
1 1.05 2.6532 .20
millones de pesos
Ejemplo. Ahora suponiendo que el inversionista desea invertir el mismo capital pero
semestralmente. En este caso el 5% anual se convierte en:
5
5% 5 1100
2 2 200 40
Al término del primer semestre retira:
1 11 (1) 1 1.025 .
40 40millones de pesos
Al término del segundo semestre retira:
2
21 1 1 1 1 11 1 1 1 1 1.025 1.506 .
40 40 40 40 40 40millones de pesos
Por lo que la cantidad que se retirará después de 20 años de inversión semestral continua
será de:
40
4011 1.025 2.6850 .
40millones de pesos
Las personas que se dedican a los negocios de dinero, buscan invertir dinero en todo
momento. Supongamos que una persona busca invertir un millón de pesos en 20 años,

53
pero a cada hora. Consideremos que en 20 años hay unas 175,320 horas; de acuerdo al
comportamiento observado en los ejercicios anteriores, retiraría en 20 años, con una
inversión por hora:
1753201
1 2.718276075 .175320
millones de pesos
Si este inversionista quisiera invertir a cada instante, la cantidad a retirar estaría dada por:
11
x
x
Si x es un número muy grande y sin importar que tan continuamente se haga la inversión,
este valor se aproximará a 2.71828182...
A la cantidad
11
n
n
cuando n es un número natural muy grande, se le representa con
la letra e y tiene un valor aproximado de 2.718281828…
2.718281828e
En el último ejemplo, se puede ver que si una persona invierte un capital con interés i
continuamente, en t años se tendrá un capital dado por
0( ) itC t C e
Ejemplo. Cotidianamente, el mercado de dinero sufre el efecto conocido como
devaluación, dependiendo en gran medida del país. Estudiosos de la economía han
encontrado que la depreciación del dinero está dada por ( ) itV t Ae
, A representa la
cantidad de dinero con que se cuenta en ese momento.
Por ejemplo si nuestra moneda sufre una devaluación del 10% anual, $50,000 se habrán
devaluado en 2 años a: (0.1)(2)(2) 50,000 40,936.53V e .

54
Ejemplo Otro caso, en el que podemos utilizar las funciones exponenciales es el
crecimiento de las bacterias. Si suponemos que las bacterias se duplican cada hora y
comenzamos a observar su crecimiento con tan sólo una bacteria se tiene que:
Antes de empezar, f(0) = 20 = 1
Después de 1 hora f(1) = 21 = 2
Después de 2 horas f(2) = 22 = 4
En 3 horas f(3) = 23 = 8
Por lo que podemos representar el crecimiento de estas bacterias con la función:
( ) 2xf x
Si damos valores a x, y los evaluamos en la función, tenemos la siguiente tabla:
x
-4 0.062
-3 0.12
-2 0.25
-1 0.50
0 1
1 2
2 4
3 8
4 16
Ejemplo.
Crecimiento de bacterias
En un experimento, se mide el número de bacterias presentes en un cultivo, al cabo de t
minutos
su comportamiento queda representado en la siguiente función:
4
( ) 3003
t
N t
Donde N (t) es un múltiplo constante de la función exponencial.
a) ¿Cuántas bacterias están presentes inicialmente?

55
El objetivo es determinar N(t) cuando t=0, por lo que debemos evaluar la función de la
siguiente manera:
04
(0) 300 300(1) 3003
N
b) Aproximadamente, ¿cuántas bacterias están presentes después de 3 minutos?
En este caso el tiempo t=3, se sustituye en la función:
34 64 6400
(3) 300 3003 27 9
N
Por lo que se concluye que después de 3 minutos, hay casi 711 bacterias presentes.
Desintegración radioactiva
Un elemento radiactivo decrece o decae de manera que después de t días, el número de
miligramos presente, M, está definido por 0.062( ) 100 tM t e . ¿Cuántos miligramos se tenían
al inicio ?, ¿cuántos miligramos se tendrán después de 20 días?
a)
0
0
.
100
0.062
0
M Cantidad inicial de miligramos
M
k
t
Por ello:
0.062(0)(0) 100 100M e
b) Cantidad de miligramos después de 10 años
0.062(10)
0.62
(10) 100
100
100(0.53794)
53.8
M e
e
Después de 10 días habrá aproximadamente 53.8 mg.

56
GRÁFICA DE LA FUNCIÓN EXPONENCIAL.
Como se mencionó, la función exponencial tiene como regla de correspondencia
, 0, 1.xy a a a
La función xxf 2)( es muy parecida a la función exponencial, que está definida como:
( ) xf x e
Esta función tiene por dominio el conjunto de los números reales. Observemos que en
estas funciones, la variable independiente es parte del exponente.
Si a la función exponencial le cambiamos la base, en la gráfica se ven representadas las
siguientes traslaciones:

57
En donde observamos que mientras más crece la base, su gráfica crece más rápido y se va
acercando más rápido a los ejes coordenados en relación a ( ) 2xf x .
Si la base de la función exponencial es menor a uno, tendremos graficas como las que se
muestran a continuación:
Se observa en la figura anterior que:
● Mientras la base es más grande, la gráfica crece más rápido.
● Todas las gráficas cortan al eje Y en el punto P (0,1) (¿puedes justificar por qué?).
● La función tiene como asíntota horizontal el eje X, es decir, se acerca cada vez más al eje
X pero sin cruzarlo.
● En todos los casos mostrados, el dominio de la función está dado por: { / }fD x x es
decir el dominio la función está definida por todos los números reales.
● El rango está dado por: { / }fR y y
● Si 0 1a la función es decreciente.
● Si 1a la función es creciente.
Recuerda que dependiendo de las traslaciones, varían los parámetros de lasa funciones
exponenciales.

58
EJEMPLOS:
Si sabemos que: ( ) 2 ;x
f ff x D R
Utilizando traslaciones verticales y horizontales, graficamos las siguientes funciones:
Ejemplo.
( ) 2 2xf x
La gráfica de la función 22)( xxf se desplaza dos unidades hacia abajo con respecto
a la función ( ) 2xf x , quedando la gráfica de la siguiente forma:
Solución: ; ( 2, )f fD R

59
Ejemplo.
El 2 que aparece sumado al exponente, permite que la gráfica se desplace 2 unidades
hacia la izquierda con respecto a la gráfica xexf )( .
Solución:
La gráfica es:
; (0, )f fD R .
En un cuadro comparativo acerca del comportamiento de la función exponencial de
acuerdo al cambio de sus parámetros, se expresan las siguientes funciones
Ejercicios resueltos.
Sean las funciones:
1 1
) ( ) 2 ) ( ) 2 ) ( ) ) ( )2 2
x x
x xa f x b f x c f x d f x
Obtener la gráfica de la función, su dominio y rango.

60
Solución
Al realizar la tabla de valores y llevar los puntos al plano cartesiano para hacer el trazo de
cada gráfica de la función, se obtiene:
) ( ) 2xa f x ) ( ) 2 xb f x
x y
-3 0.125
-2 0.25
-1 0.5
0 1
1 2
2 4
3 8
x y
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
; (0, )f fD R ; (0, )f fD R
¿Qué es lo que cambia en la función?______________
¿Cuál es el efecto aplicado en la gráfica asociada a cada función?_________________
En contraste
1) ( )
2
x
c f x
1
) ( )2
x
d f x
x y
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
x y
-3 0.125
-2 0.25
-1 0.5
0 1
1 2
2 4
3 8
; (0, )f fD R ; (0, )f fD R
¿Qué es lo que cambia en la función?______________

61
¿Cuál es el efecto aplicado en la gráfica asociada a cada función?_________________
En comparación con las gráficas de los incisos a y b, ¿los cambios ocurridos en las
gráficas de las funciones ocurren de igual manera?___________________
EJERCICIOS:
1. Si una cantidad 0C se invierte durante t años con un interés anual compuesto del r %,
se calcula que la cantidad a retirar está dada por: 0( ) 1100
ntr
C t Cn
Donde n es el
número de veces que la cantidad 0C se reinvierte en un año.
Por ejemplo, si se reinvierten $50,000 al 6% anual compuesto durante 2 años, reinvertidos
mensualmente sin hacer retiros, al término del período la cantidad a retirar será:
12(2)
6(2) 50,000 1 56,357.98
100(12)C
Determina la cantidad a retirar, bajo las mismas condiciones si:
a) Se invierte durante 5 años trimestralmente.
R=67,342.75
b) Se invierte durante 5 años semestralmente.
R=67,195.81
Recuerda que si la inversión se hace continuamente es más conveniente usar
0( ) ntC t C e .
c) Usando esta última fórmula determina el capital a retirar después de 6 años al 6% anual.
R=$71,666.47
2. La mamá de Lalo abrió una cuenta bancaria para su hijo con $100 cuando él nació. La
cuenta gana interés a una tasa de 30% al año, mensual. Si no se deposita ni se retiró
dinero de la cuenta, ¿cuánto dinero habrá en la cuenta cuando Lalo cumpla 18 años?
R:Aproximadamente $20718.33

62
3. El modelo aproximado de Jenns: 3.379 6 xy x e , es considerado el más preciso para
determinar la estatura de los niños menores de 7 años. Si y es la estatura medida en
centímetros, x es la edad medida en años: ¿Cuál debe ser la estatura de un niño de 5
años?
R=108.81
cm.
4. Poco después de consumir una dosis sustancial de whisky, el nivel de alcohol en la
sangre de una persona sube a un nivel de 0.3 miligramos por mililitro (mg/ml). De ahí en
adelante, este nivel decrece de acuerdo con la fórmula ( ) 0.3(0.5)tA t , dónde t es el tiempo
medido en horas a partir del instante en que se alcanza el nivel más alto. ¿Podrá esta
persona conducir su automóvil después de dos horas, tomando en cuenta que para
conducir legalmente su automóvil en su localidad el límite legal es de 0.08 mg/ml de alcohol
en la sangre?
R= En 2 horas tendrá 0.075mg/ml.
Si podrá conducir.
5. Supongamos que se invierten $1000 durante 8 años a una tasa anual compuesto
semestralmente. Calcula el monto.
R= $1992.56
6. Una persona debe la cantidad de $6000 pesos en su tarjeta de crédito que cobra una
tasa de interés anual de 36%. Si no realiza ningún pago y el banco capitaliza los intereses
trimestralmente, ¿cuánto deberá pagar al cabo de 2 años?
R= $11,955.37 pesos
7. Una población de 4 millones de habitantes crece a una tasa de 3% anual. Calcule el
tamaño de la población al término de 5 años.
R= 4.63 millones de habitantes
8. La población de cierta nación en desarrollo se determinó que está dada por medio de la
fórmula , donde t representa el número de años medidos a partir de 1960.

63
Determine la población en un 1980 y la población proyectada en el año 2000, suponiendo
que esta fórmula continúe siendo válida hasta el día de hoy.
R= En 1980, 22.4. En el año 2000, 33.4
9. En 1938, en cierto país, se promulgó una ley federal que establecía un salario mínimo y
éste fue de $0.25 por hora; el salario había subido a $5.15 por hora en 1997. Se pide
encontrar la función exponencial de la forma ty ab que modele el salario mínimo federal
para 1938-1997
R= El modelo es 0.25(1.0526)ty

64
FUNCIONES LOGARITMICAS
El concepto de función tiene múltiples usos. Si nos centramos en las matemáticas, una función es una relación que existe entre dos conjuntos, mediante la cual a cada elemento del conjunto inicial se le asigna un solo elemento del conjunto final (o ninguno). Logarítmico, por su parte, es aquello vinculado a un logaritmo: el exponente al cual se necesita elevar una cierta cantidad para obtener como resultado un número determinado.
Una función logarítmica es aquella que se puede representar de la forma:
( ) logbf x x
En estas funciones, b es la base, que tiene que ser positiva y diferente de 1. La
forma oficial de leer esta ecuación es la siguiente: “la función de x es igual al logaritmo base b de x”.
Es importante mencionar que la función logarítmica es la función inversa de la función exponencial: aquella que se representa con la ecuación f(x) = bˣ
Entre las principales características de una función logarítmica, podemos mencionar que su dominio (su conjunto de partida o inicial) son los números reales positivos. Se trata de una función continua, cuyo recorrido es R (las imágenes que se obtienen de aplicar la función corresponden a cualquiera de los elementos del conjunto formado por los números reales).
Las funciones logarítmicas, por otra parte, pueden ser crecientes o decrecientes, según el valor de la base.

65
La gráfica de la función logarítmica ( ) log( )f x x
(Nota: al no aparecer el subíndice correspondiente a la base de la función significa que la base es 10)
En las siguientes gráficas, observa cómo es que al variar la base de la función, la gráfica se va modificando

66
Como puedes observar, entre más grande sea el valor de la base, la gráfica tiende a acercarse cada vez más al eje de las abscisas, y entre más pequeño es el valor de la base la gráfica se aleja cada vez más. Puedes notar que todas las gráficas intersectan al eje de las x en el valor de 1, no importando la base que estén manejando. Otra característica que se puede observar en la gráfica es que al no existir el logaritmo de cero, la gráfica tiene una asíntota en ese valor, por lo que se va acercando al eje de las ordenadas sin llegar a cruzarlo. Ahora, veamos qué es lo que pasa con la gráfica cuando le agregamos un signo negativo: La gráfica de la función ( ) log( )f x x se muestra a continuación:
Como puedes observar, al cambiar el signo a la función, está aparece ahora invertida con respecto al eje de las abscisas, conservando la misma forma pero en diferente posición. Puedes notar que al igual que en las gráficas anteriores sigue intersectando a x en el valor de 1 y que en la parte superior sigue creciendo y acercándose cada vez más al eje de las ordenadas.

67
Veamos ahora, que es lo que pasa si al valor de x le cambiamos de signo, es decir la función ahora será : ( ) log( )f x x
Como se menciona en la definición, no existen los logaritmos para números negativos, sin embargo, al tabular la función anterior se asignan solo valores negativos para la variable x, con lo cual si se pueden obtener los valores de los logaritmos y origina que ahora la gráfica aparezca hacia la izquierda en el plano cartesiano. Observa que guarda la misma forma que las gráficas anteriores, sólo que la dirección cambia y ahora intersecta al eje de las abscisas en -1. Además puedes observar que en la parte inferior sigue creciendo y acercándose cada vez más al eje de las ordenadas.

68
Ahora, si modificamos ambos signos a la vez, es decir si la función a graficar ahora es ( ) log( )f x x la gráfica correspondiente queda de la siguiente manera:
Observa, como de nueva cuenta la gráfica se invierte en cuanto a posición con respecto al eje de las abscisas y la dirección sigue igual que en la anterior por el signo negativo de x. Observa también que la intersección con el eje de las abscisas es en el valor de x igual a -1. En resumen: La función logarítmica es aquella cuya expresión es de la forma: ( ) logf x x , el
valor de x debe ser un número positivo y diferente de cero, y cambia su grafica de acuerdo a los siguientes parámetros:
Forma de la ecuación Comportamiento
( ) logf x x Es creciente hacia la derecha, pasa por x=1.
( ) logf x x Es decreciente hacia la derecha pasa por x=1.
( ) log( )f x x Es creciente hacia la izquierda, pasa por x =-1.
( ) log( )f x x Es decreciente hacia la izquierda, pasa por x = -1.

69
Ahora, la expresión algebraica de una función logarítmica también puede cambiar y presentarse de la siguiente manera:
( ) log( 4)f x x
La gráfica correspondiente a la función es:
Como se puede observar, la gráfica de la función logarítmica aparece desplazada horizontalmente hacia el lado izquierdo, hacia los valores negativos del eje x, el valor que hace que el logaritmo no se pueda calcular es el de x = -4 ya que da como resultado cero al sustituirlo y por lo tanto en ese lugar se puede apreciar una línea punteada indicando que ahí no existe la función. Se puede apreciar también que una unidad a la derecha, como en las gráficas anteriores, la función cruza al eje de las abscisas.

70
Veamos ahora la siguiente función:
( ) log( 3)f x x
La gráfica correspondiente a la función es:
Podemos observar ahora que la gráfica se encuentra desplazada hacia la derecha, hacia el lado positivo del eje x, el valor que hace que el logaritmo no se pueda calcular es el de x = 3, ya que da como resultado cero y está representado con una línea punteada indicando que ahí no existe la función, además la gráfica intersecta al eje de las abscisas una unidad a la derecha como en las gráficas anteriores.

71
Tenemos ahora la siguiente función:
( ) log( ) 5f x x
La gráfica correspondiente a la función es:
Observa, la función ahora aparece desplazada hacia arriba, es decir, al lado positivo del eje de las ordenadas, observa como aparece una línea punteada de referencia en la cual se puede observar como la gráfica es creciente y a la altura del eje de referencia lo intersecta una unidad a la derecha como en los ejemplos anteriores.

72
Trabajemos ahora la siguiente función:
( ) log( ) 2f x x
La gráfica correspondiente a la función es:
La función se encuentra desplazada hacia abajo, hacia los valores negativos del eje de las ordenadas, aparece una línea punteada de referencia en la cual se puede observar como la gráfica comienza a ser creciente y a esa altura e intersecta al eje de referencia una unidad a la derecha como en los ejemplos anteriores. Por lo tanto, podemos resumir los comportamientos de la función logarítmica en la siguiente tabla:
Forma de la ecuación
Comportamiento
( ) log( )f x x a La gráfica de la función se desplaza horizontalmente hacia la derecha
( ) log( )f x x a La gráfica de la función se desplaza horizontalmente hacia la izquierda
( ) log( )f x x b La gráfica de la función se desplaza verticalmente hacia abajo
( ) log( )f x x b La gráfica de la función se desplaza verticalmente hacia arriba

73
Una vez analizados los elementos y el comportamiento de cada uno de ellos en la función logarítmica se facilita la ubicación de la función racional en el plano cartesiano, es decir: Ejemplo: Elabora la gráfica de la función ( ) log( 4) 3f x x
Solución: Se puede observar que la función que se va a graficar tiene como base al número 10, es un logaritmo positivo, por lo que se considera creciente y el valor de x es positivo, por lo tanto se dirige hacia la derecha. El valor de – 4 desplaza la gráfica de la función cuatro unidades horizontalmente a la derecha, el valor de +3 indica que la gráfica será desplazada tres unidades verticalmente hacia arriba. La gráfica de la función queda de la siguiente manera:
Veamos otro ejemplo. Elabora la gráfica de la función ( ) log( 2) 4f x x
Solución: Se puede observar que hay un signo negativo acompañando al logaritmo, el cual ocasiona que ahora la gráfica sea decreciente hacia la derecha, la base del logaritmo es 10 al no aparecer subíndice acompañando al logaritmo.

74
El valor que acompaña a x, el +2 indica que la gráfica estará desplazada 2 unidades a la izquierda, hacia el lado negativo del eje de abscisas, el valor de -4 ocasiona que la gráfica se desplace cuatro unidades hacia abajo, al lado negativo del eje de las ordenadas. Con estos elementos, la gráfica de la función queda de la siguiente manera:
Ejercicios Realiza el bosquejo de la gráfica de las siguientes funciones logarítmicas
1) ( ) log( 6) 4f x x
2) ( ) log( 3) 2f x x
3) ( ) log ( 4) 5f x x
4) ( ) log ( 3) 1f x x
5) 3
( ) log 22
f x x
6) 7
( ) log 42
f x x

75
Respuestas a los ejercicios: a)
b)
c)

76
d)
e)
f)

77
ECUACIONES EXPONENCIALES.
Una ecuación exponencial es una expresión algebraica cuya incógnita x se
encuentra en el exponente.
Ejemplo 1: Resolver 3 27x .
Observemos que la x se encuentra en el exponente. El 27, se puede expresar
como el siguiente producto:
3
27 3 3 3
27 3
Por lo que, la ecuación queda como: 33 3x
Como la base es la misma, los exponentes deben ser iguales, por lo que: 3x
Ejemplo 2. Resolver 22 16x
El 16 se puede expresar como el siguiente producto:
4
16 2 2 2 2
16 2
Por lo que, la ecuación queda como:
2
4 2
16 2
2 2
x
x
Igualando exponentes se obtiene:
2 4
4 2
2
x
x
x

78
Ejemplo 3: Resolver 2
12 64x
Escribimos 64 como una potencia de 2:
6
64 2 2 2 2 2 2
64 2
aplicando leyes de exponentes tenemos que: 2 2
2 2 6
2 64
2 2
x
x
Igualando exponentes:
2 2 6
2 6 2
2 4
4
2
2
x
x
x
x
x
Ejemplo 4. Resolver 1 12 2 20x x
Aplicando las propiedades de las potencias:
1 1
1 1
2 2 2 2 2;
22 2 2
2
x x x
xx x
Con lo que podemos reescribir la ecuación como
22 2 20
2
xx

79
Observemos que 2x es un factor común, por lo que:
3
12 2 20
2
4 12 20
2
52 20
2
22 20
5
2 8 2
x
x
x
x
x
Por lo que se concluye que la solución es 3x .
Ejemplo 5. Resolver
81
22
x
.
Convertimos
81
2
x
a base 2.
8
81
8
12
2
2 2
8 1
9
xx
x
x
x

80
Ejemplo 6. Resolver 3 44 8x x
3
3 2 3
4
44 3
42 3 3
2 6 12 3
4 2.
4 (2 )
8 2
8 2
:
(2 ) 2
2 2
exp :
2 6 12 3
5 18
18
5
x
x x
x
xx
xx
x x
Convertimos a base
Convertimos a base
Igualamos
Igualando onentes tenemos que
x x
x
x
Ejemplo 7. Resolver 50 5 12 (0.5)x x
5 1 1 5 1 5 1
5 150
0.5 2.
(0.5) (2 ) 2
2 2
exp :
50 5 1
45 1
1
45
x x x
xx
Convertimos a base
por lo que
Igualamos onentes
x x
x
x

81
Ejercicios: Resuelve las siguientes ecuaciones exponenciales
1. 2 2 13 3 12x x R: 2x
2. 7 2 16 6x x R: 2x
3. 3 416 8x x R:
24
7x
4. 310 1x R: 3x
5. 100 42 (0.5)x x R: 4
99x
6. 1 34 2 320x x R: 3x
7. 1 17 49x x R: 1x
8.
61
22
x
R: 7x
9. 2
2 33 3xx
R: 3, 1x x
,
10.
3 2
2 18(2 ) 4
2
x
x x
R: 3x
II. Realiza la gráfica de las siguientes funciones y obtén dominio y rango:
a) ( ) xf x e b) ( ) xf x e c) ( ) xf x e
d) ( ) 2 xf x e e) 2( ) xf x e f)
3( ) xf x e
g) 4 1( ) xf x e h) ( ) 2xf x e i)
2( ) xf x e
j) 3( ) 2 4xf x e

82
Solución
a) ( ) xf x e
b) ( ) xf x e
c) ( ) xf x e
d) ( ) 2 xf x e
e) 2( ) xf x e
f) 3( ) xf x e
g) 4 1( ) xf x e
h) ( ) 2xf x e
i) 2( ) xf x e
j)
3( ) 2 4xf x e

83
Resuelve las siguientes ecuaciones y problemas.
1. R:
2. R:
3. Después de tomar un medicamento líquido la concentración del medicamento
en la sangre es de 0.2 mg/dl si esa cantidad decae de acuerdo a y
cada hora se absorbe la cuarta parte ¿Cuánto tardará en que la concentración del
medicamento en la sangre sea de 0.08 mg/dl?
Respuesta 0.66 horas
4. Un anestésico para animales llamado pentobarbital sódico se usa para un perro
y se requieren 30 mg por Kg. de peso del perro a tratar. El anestésico se elimina
de acuerdo a .En 4 horas la cantidad suministrada disminuye a la mitad.
Calcula la cantidad a suministrar para anestesiar a un perro de 20 Kg. durante 45
minutos.
Respuesta = 683.3 mg

84
LOGARITMOS
Logaritmo base b de un número y su relación con la potencia base b
La ecuación yx b nos dice que y es el exponente de b que produce x. En
casos como éste se usa la palabra logaritmo en lugar de exponente. Ahora,
podemos decir que y es el logaritmo de b que produce x. Esta descripción se
abrevia con logby x , de ahí que es das formas expresan lo mismo, y como
son equivalentes, definen la misma función.
En ocasiones es útil convertir una función logarítmica a la forma exponencial,
cuando se realiza su gráfica, por ello a continuación veremos cómo se realiza este
procedimiento.
Ejemplo 1
Convertir la expresión 4logy x a su equivalente en forma exponencial.
Utilizando la equivalencia anterior tenemos lo siguiente:
4logy x utilizandoyx b
4yx
Si tabulamos ambas expresiones, obtenemos los mismos valores, puesto que
ambas definen a la misma función.
Ejemplo 2:
Convertir la expresión 3log 1y x a su equivalente en forma exponencial.
Utilizando la equivalencia xx b tendríamos lo siguiente:
3log 1y x
1 3
3 1
y
y
x
x
Ejemplo 3:
Convertir la expresión 10log 3 5y x a su equivalente en forma
exponencial.

85
Utilizando la equivalencia xx b tendríamos lo siguiente:
10log 3 5y x
10
10
5
5
log 3 5
5 log 3
3 10
10 3
y
y
y x
y x
x
x
Ejercicios.
Convertir las siguientes expresiones logarítmicas a su equivalente en forma
exponencial.
1) 6log 5y x
2) 13
log 2y x
3) 100logy x
4) 15log 5 10y x
5) 25
log 9y x
Respuestas:
1) 56yx
2) 1
23
y
x
3) 100yx

86
4) 1015 5yx
5)
92
5
y
x
PROPIEDADES DE LOS LOGARITMOS
Cambio de base
Para 0N y a y b siendo números reales positivos diferentes de 1:
loglog
log
ab
a
NN
b
Leyes de los logaritmos
Si M y N son positivos, b > 0 y b 1, entonces:
Ley 1. log log logb b bNM M N
Ley 2. log log logb b b
MM N
N
Ley 3. log logk
b bN k N
Ejemplo 1
Con la fórmula para el cambio de base y una calculadora determina el siguiente
logaritmo, redondea tu resultado a cuatro cifras decimales.
4log 120
Al resolverlo en la calculadora obtenemos el valor de 3.4534
Ahora, utilizando logaritmos base 10 y aplicando la fórmula para el cambio de
base
loglog
log
ab
a
NN
b

87
Obtenemos los siguiente:
104
10
log 120 2.0792log 120 3.4532
log 4 0.6021
Ejemplo 2
Convertir la siguiente expresión en el logaritmo de una expresión única de x, en su
forma simplificada.
3log log 2 log 5b b bx x
Comenzaremos aplicando la tercera ley log logk
b bN k N para eliminar
coeficientes:
3log log 2 log 5b b bx x
Es importante mencionar que, si se tuviera distinta base, será necesario primero
aplicar la fórmula para cambio de base. A continuación, como tenemos diferencia
de logaritmos, se aplicará la segunda ley log log logb b b
MM N
N en dos
ocasiones:
3
log log 52
b b
xx
3
2log5
b
x
x
Simplificando la expresión anterior tenemos:
3
log2 5
b
x
x

88
Ejemplo 3
Convertir la siguiente expresión en el logaritmo de una expresión única de x, en su
forma simplificada.
1 1
log 1 log 3 log 13 3
b b bx x
Comenzaremos aplicando la tercera ley log logk
b bN k N para eliminar
coeficientes:
1 1
3 3log 1 log 3 log 1b b bx x
Es importante mencionar que, si se tuviera distinta base, será necesario primero
aplicar la fórmula para cambio de base. A continuación, como tenemos suma de
logaritmos, se aplicará la primera ley log log logb b bNM M N :
1 1
3 3log 3 1 log 1b bx x
Después, al tener una diferencia de logaritmos, aplicaremos la segunda ley
log log logb b b
MM N
N :
13
13
3 1log
1b
x
x
Finalmente, simplificando la expresión anterior, aplicando leyes de los exponentes
y radicales tenemos:
13
3
1log 3
1
1log 3
1
b
b
x
x
x
x

89
Ejemplo 4
Convertir la siguiente expresión en el logaritmo de una expresión única de x, en su
forma simplificada.
log 2log 1a bx x
En este ejemplo, se puede observar que tenemos distinta base en la expresión;
por o tanto será necesario aplicar la fórmula de cambio de base log
loglog
ab
a
NN
b , lo
primero que se debe definir es la base con la que se va a trabajar, supongamos
que queremos utilizar la base b:
log
2log 1log
bb
b
xx
a
La expresión logb a es una constante, por lo tanto, podemos separarla de la
siguiente manera, para poder aplicar la tercera ley de los logaritmos
log logk
b bN k N en ambos términos de la expresión.
1
log 2log 1log
b b
b
x xa
1 2
loglog log 1b ab bx x
Finalmente, aplicando la primera ley de los logaritmos
log log logb b bNM M N , obtenemos lo siguiente:
1 2
loglog 1b ab x x
Y simplificando la expresión anterior tenemos:
loglog 1b a
b x x

90
Ejemplo 5
Utiliza las leyes de los logaritmos para convertir el siguiente logaritmo a una
expresión donde intervengan sumas, diferencias y múltiplos de logaritmos.
2 1logb
x
x
Podemos observar que se presenta una raíz cuadrada, por lo tanto, aplicando las
leyes de los exponentes y radicales, podemos expresarla de la siguiente manera:
1
2 21logb
x
x
A continuación, se aplicará la segunda ley de los logaritmos
log log logb b b
MM N
N para expresar el logaritmo de una división como la
diferencia de logaritmos:
1
2 2log 1 logb bx x
Finalmente, se aplicará la tercera ley de los logaritmos log logk
b bN k N
para eliminar el exponente:
21log 1 log
2b bx x
Ejercicios
1. Con la fórmula para el cambio de base y una calculadora determine cada uno de
los siguientes logaritmos, redondeando a cuatro cifras decimales.
a) 5log 95
b) 8log 64
c) 12log 257

91
2. Convertir cada expresión en el logaritmo de una expresión única de x, en su forma
simplificada.
a) log 1 log 2b bx x
b) 2log 2 log 4b bx x
c) 2 21 1log 1 log 1
2 2b bx x
d) 23log loga bx x
3. Usando las leyes de los logaritmos, convertir los logaritmos en expresiones donde
intervengan sumas, diferencias y múltiplos de logaritmos.
a)
2
log1
b
x
x
b) 2
1logb
x
c) 1
log1
b
x
x
d) 3
2 5logb
x
x
Respuestas
Ejercicio 1.
a) 2.8295
b) 2
c) 2.2331
Ejercicio 2.
a) 2log 3 2b x x
b) 1
log2
bx

92
c)
2
2
1log
1b
x
x
d) log 3 2log b a
b x x
Ejercicio 3.
a) 2log log 1b bx x
b) log 1 2logb b x
c) 1 1
log 1 log 12 2
b bx x
d) log 2 5 3logb bx x
Logaritmo natural
La expresión 1
1
n
n
, en la cual n representa un entero positivo, desempeña un
papel importante en el estudio del cálculo infinitesimal. Con ayuda de la siguiente
tabla podemos observar qué sucede cuando el valor de n crece hasta infinito:
n 1
1
n
n
1 2.0000000
10 2.5937425
100 2.7048138
1000 2.7169239
10000 2.7181459
100000 2.7182682
1000000 2.7182805
De acuerdo con los resultados de esta tabla, parece que los valores de la
expresión aumentan y se acercan a 2.71828. De hecho, en cálculo infinitesimal se

93
puede demostrar que 1
1
n
n
tiende a un número específico que se representa
mediante la letra e.
Al igual que el número , e es un número irracional, su representación decimal es
no terminal y no repetitiva, y es la base más importante de las funciones
exponenciales y logarítmicas.
La función inversa de xy e es logey x . En lugar de loge x se acostumbra
escribirlo como ln x . Las leyes de los logaritmos, son aplicables también en el
caso del logaritmo natural.
Ejemplo 1
Convertir la siguiente expresión en el logaritmo natural de una expresión en x.
2 21ln 1 ln 2 ln 1
2x x x x
Comenzaremos aplicando la tercera ley log logk
b bN k N para eliminar
coeficientes:
1
2 22ln 1 ln 2 ln 1x x x x
Es importante mencionar que, si se tuviera distinta base, será necesario primero
aplicar la fórmula para cambio de base. A continuación, como tenemos una
diferencia de logaritmos, se aplicará la segunda ley log log logb b b
MM N
N :
12 2
2
1ln ln 1
2
xx
x x

94
Posteriormente, como tenemos una suma de logaritmos, aplicaremos la primera
ley log log logb b bNM M N
12 2
2
1ln 1
2
xx
x x
Factorizando y simplificando la expresión anterior tenemos:
12 21
ln 12 1
xx
x x
12 2 21 1
ln2 2
x x
x x
Ejemplo 2
Utiliza las leyes de los logaritmos para convertir el siguiente logaritmo natural, en
una expresión donde intervengan sumas, diferencias y múltiplos de logaritmos
naturales.
2
2
3ln
4
x
x
Se aplicará la segunda ley de los logaritmos log log logb b b
MM N
N para
expresar el logaritmo de una división como la diferencia de logaritmos:
2 2ln3 ln 4x x
A continuación, se aplicará la primera ley de los logaritmos
log log logb b bNM M N para expresar el logaritmo de un producto como
una suma de logaritmos:
2 2ln3 ln ln 4x x

95
Finalmente, se aplicará la tercera ley de los logaritmos log logk
b bN k N para
eliminar el exponente:
2ln3 2ln ln 4x x
Ejercicios
1. Convertir cada expresión en el logaritmo de una expresión única de x, en su forma
simplificada.
a) 21ln ln 5
2x x
b) 3ln 1 3ln 1x x
c) 21 1ln 2 2ln 1 ln 1
2 3x x x
d) ln 2 ln ln 1x x
2. Usando las leyes de los logaritmos, convertir los logaritmos en expresiones donde
intervengan sumas, diferencias y múltiplos de logaritmos naturales.
a) 2
5ln
4
x
x
b) 2ln 1x x
c) 7
ln7
x
x
d)
2
2
1 3ln
2
x x
x

96
Respuestas
Ejercicio 1.
a) 2ln 5x x
b) 3 3ln 1 1x x
c)
23 2
2ln
1 1
x
x x
d) 2
ln1
x
x
Ejercicio 2.
a) ln5 ln ln 2 ln 2x x x
b) 21ln ln 1
2x x
c) 1 1
ln 7 ln 72 2
x x
d) 21ln 1 3ln 3 ln 2
2x x x
ECUACIONES LOGARÍTMICAS
Para resolver ecuaciones logarítmicas se aplican las leyes de los logaritmos hasta
obtener el logaritmo de una expresión única de x.
Ejemplo 1
Obtener el valor de x, comprobar el resultado.
log 21 log 2x x
En el primer miembro de la ecuación aplicamos la primera ley de los logaritmos
log log logb b bNM M N y obtenemos lo siguiente:
2
log 21 2
log 21 2
x x
x x

97
Recordando que logby x equivale a yx b tenemos lo siguiente:
2 221 10x x
La expresión anterior es una ecuación cuadrática la cual resolveremos por
factorización:
2 2
2
1
2
21 10
21 100 0
25 4 0
25
4
x x
x x
x x
tenemos
x
x
Para realizar la comprobación, se sustituyen los valores obtenidos en la ecuación
y se verifica la igualdad, el primer valor obtenido no puede ser la solución, puesto
que no existe el logaritmo de un número negativo, así que solo utilizamos la
segunda solución.
Solución 2 2 4x
log 21 log 2x x
log 4 21 log 4 2
log 25 log 4 2
log 25 4 2
log100 2
2 2
Ejemplo 2
Obtener el valor de x, comprobar el resultado.
log 3 log 12 1x x

98
En el primer miembro de la ecuación, se aplica la segunda ley de los logaritmos
log log logb b b
MM N
N y obtenemos lo siguiente:
3log 1
12
x
x
Recordando que logby x equivale a yx b tenemos lo siguiente:
1310
12
x
x
La expresión anterior es una ecuación lineal, la cual se resolverá de la siguiente
manera:
3 0.1 12
3 1.2 0.1
0.1 1.2 3
0.9 1.8
1.8
0.9
2
x x
x x
x x
x
x
x
Para realizar la comprobación, se sustituye el valore obtenido en la ecuación y se
verifica la igualdad.
Solución 2x
log 3 log 12 1x x
log 3 2 log 12 2 1
log 1 log 10 1
1log 1
10
log 0.1 1
1 1

99
Ejemplo 3
Obtener el valor de x, comprobar el resultado.
2ln 4 ln 2 0x x
En el primer miembro de la ecuación, se aplica la segunda ley de los logaritmos
log log logb b b
MM N
N y obtenemos lo siguiente:
2 4ln 0
2
x
x
Factorizando y simplificando la expresión anterior obtenemos:
2 2ln 0
2
ln 2 0
x x
x
x
Recordando que logby x equivale a yx b tenemos lo siguiente:
02
2 1
x e
x
La expresión anterior es una ecuación lineal, la cual se resolverá de la siguiente
manera:
2 1
1 2
3
x
x
x
Para realizar la comprobación, se sustituye el valor obtenido en la ecuación y se
verifica la igualdad.
Solución 3x
2ln 4 ln 2 0x x

100
2ln 3 4 ln 3 2 0
ln 9 4 ln 5 0
ln 5 ln 5 0
0 0
Ejercicios
Obtener el valor de x de las siguientes ecuaciones logarítmicas:
a) log log5 2x
b) 12 12log 5 log 5 2x x
c) log log5 1x
d) 2
2 2log log 2 3x x
e) ln ln 2 1x
f) ln 2 ln 1x x
g) ln 1 0x
h) 2ln 2 ln ln 1x x x x
Respuestas
a) 20x
b) 1
2
17
7
x
x
c) 2x
d) 4x
e) 1.3591409142
ex
f) 1.135343x
g) 0x
h) 1x

101
Resolución de problemas de aplicación
Ejemplo 1
Una sustancia radioactiva se desintegra siguiendo la fórmula exponencial
0.04
0
tS S e donde S es la cantidad de sustancia en gramos, S0 es la cantidad de
sustancia inicial en gramos y t es el tiempo en años. Si había 50 gramos de la
sustancia radioactiva al principio, ¿en cuánto tiempo decaerá a la mitad?
Para resolver el problema debemos despejar a la variable t, y sustituir la
información proporcionada, comenzaremos con la sustitución:
0.0425 50 te
A continuación, despejaremos la variable t, como la base exponencial es e,
utilizaremos el logaritmo natural.
0.04
0.04
0.04
25 50
25
50
0.5
ln 0.5 0.04
ln 0.5
0.04
17.32
t
t
t
e
e
e
t
t
t
Por lo tanto, la respuesta es 17.32 años.

102
Ejemplo 2
La señora González deposita $5000.00 al 9% anual. ¿Cuánto tiempo pasará para
que su depósito duplique su valor? ¿Cuánto tiempo pasaría si el interés fuera del
12% anual? En ambos casos suponga capitalización continua.
La fórmula de interés compuesto continuo es:
rtA Pe
Donde:
A = cantidad total después de t años
P = Inversión inicial
r = tasa anual de interés, como fracción decimal
t = Número de años de la inversión
De acuerdo a los datos proporcionados realizamos la sustitución en la fórmula y
despejamos al tiempo utilizando logaritmo natural.
0.09
0.09
0.09
10000 5000
10000
5000
2
ln 2 0.09
ln 2
0.09
7.7
t
t
t
e
e
e
t
t
t
0.12
0.12
0.12
10000 5000
10000
5000
2
ln 2 0.12
ln 2
0.12
5.8
t
t
t
e
e
e
t
t
t
De acuerdo a lo anterior, para una tasa del 9% el tiempo es de 7.7 años y para
una tasa del 12% el tiempo es de 5.8 años.
Ejemplo 3

103
Una sustancia radiactiva decae (se transforma en otro elemento) siguiendo la ley
0.2xy Ae , en la que y es la cantidad de sustancia presente después de x años.
Si la cantidad inicial es de 80 gramos, ¿Cuánto quedará después de 3 años?
Para resolver el problema únicamente sustituimos la información en la ley y
obtenemos la cantidad final.
0.2
0.2 3
0.6
80
80
43.905
xy Ae
y e
y e
y
Por lo tanto, la cantidad de sustancia después de tres años será de 43.905
gramos.
Ejemplo 4
Se analiza el esqueleto de un animal y se ve que contiene la tercera parte de su
14C original. ¿Qué edad tiene el esqueleto?
El carbono 14, que se representa con 14C, es un isótopo radioactivo del carbono
cuya vida media es, aproximadamente 5750 años.
Si calculamos cuánto 14C contienen los restos de un organismo que vivió hace
mucho tiempo, es posible determinar qué porcentaje corresponde a la cantidad
original de 14C cuando murió. Una vez conocida esta información, la fórmula
kxy Ae nos permite fechar la edad de los restos. La datación se hace después de
determinar la constante k. Como la cantidad de 14C después de 5750 años es 2
A
podemos calcular la constante k de la siguiente manera:

104
(5750)
5750
5750
2
2
1
2
kx
k
k
k
y Ae
AAe
A
eA
e
ln 0.5 5750
ln 0.5
5750
0.0001205
k
k
k
Conociendo el valor de la constante k, y sabiendo que el esqueleto del animal
contiene la tercera parte de su 14C original, la edad del esqueleto se calcula de la
siguiente manera:
ln 0.5 5750
ln 0.5 5750
ln 0.5 5750
1
3
3
1
3
kx
x
x
x
y Ae
A Ae
A
eA
e
1
1 ln 0.5ln
3 5750
ln 3
ln 0.5 5750
ln 35750
ln 0.5
9113.5344
x
x
x
x
De acuerdo a lo anterior, el esqueleto tiene alrededor de 9000 años de
antigüedad.
Ejercicios
1. Al estudiar el crecimiento de la población de cierta ciudad por primera vez, se
determinó que la población P, crece en función del tiempo t (años) de acuerdo con
la fórmula 0.016322000 10 tP . ¿Cuánto tiempo pasará para que la ciudad tenga
el doble de su población actual?

105
2. Se analizó una momia egipcia y se encontró que contenía el 60% de su 14C
original. Calcule la antigüedad de la momia, con precisión de 100 años. (Si A es la
cantidad original de 14C entonces lo que queda es 3/5 de A. Véase el ejemplo 4).
3. Una inversión de $1000.00 gana interés a una tasa anual r%, compuesto
continuamente. Si la inversión se duplica en 5 años, ¿Cuánto vale R? (sugerencia,
revisar el ejemplo 2).
4. Una inversión de $5000.00 gana interés a una tasa anual del 8.4%, compuesto
mensualmente. ¿Cuál es el valor de inversión después de 1 año y después de 10
años? (La fórmula del interés compuesto es 1
ntr
A Pn
donde A es el valor
final después de t años, P es la inversión inicial, r es la tasa de interés anual como
fracción decimal, n es el número de periodos anuales de capitalización y t el
número de años de la inversión).
5. Supóngase que se disuelve azúcar en agua de tal modo que el azúcar, no disuelta
es ( ) ktS t Ae , siendo A la cantidad inicial de azúcar y t la cantidad de horas
después de agregar el azúcar al agua. Si se agregaron 5 libras de azúcar y se
disolvieron 2 libras en dos horas, ¿Cuánto tiempo pasa para que se disuelva el
75% del azúcar?
Respuestas
1. 18.47 años
2. 4237.55 años, o bien, con precisión de 100 años, sería 4200 años
3. 13.86%
4. $5,437.00 después de 1 año y $11,548.00 después de 10 años.
5. 5.43 horas

106
UNIDAD 4. FUNCIONES TRIGONOMETRICAS
Propósito: Al finalizar la unidad el alumno comprenderá la extensión del concepto de razón trigonométrica a función trigonométrica. Estudiará las funciones seno y coseno en su forma característica de variación y análisis de sus parámetros. Modelara situaciones de comportamiento periódico para resolver problemas. APRENDIZAJES
Con relación a los conocimientos y destrezas, el alumno en función de la resolución de problemas:
- Explorará situaciones o fenómenos de variación periódica.
- Convertirá medidas angulares de grados a radianes y viceversa
- El alumno comprenderá la forma en que se extienden o generalizan las razones
trigonométricas para ángulos arbitrarios.
- Extenderá el concepto de razón trigonométrica a función, mediante la elaboración de una tabla o gráfica de: f(x) = sen x , f(x) = cos x
- Analizará e identifica los parámetros que aparecen en las funciones:
( ) ( )
( ) cos( )
f x Asen bx c d
f x A bx c d
D desplazamiento vertical, A amplitud, B frecuencia, y desfasamiento.
- Utilizará las funciones trigonométricas para representar fenómenos de variación periódica

107
FUNCIONES TRIGOMÉTRICAS
En la naturaleza hay gran diversidad de fenómenos que se caracterizan por su periodicidad. Estos fenómenos son los fenómenos periódicos del sonido, la luz, movimientos planetarios etc. Las funciones trigonométricas son las herramientas matemáticas básicas para analizar y describir estos fenómenos. Para ello deberás recordar algunos conceptos básicos como: Ángulos: está definido como un espacio comprendido entre dos rectas que se cortan, existen ángulos positivos y negativos como se muestra en la figura. Los positivos van en dirección contraria a las manecillas del reloj, y los negativos en la misma dirección que las manecillas del reloj:
Medida de ángulos: existen dos sistemas utilizados para medir ángulos. El sistema más empleado es la Medida en grados. En este sistema la unidad es el grado, igual al ángulo central que subtiende un arco cuya longitud es igual a 1/360 de la longitud de la circunferencia. El grado se subdivide en 60 minutos, el minuto en 60 segundos. Los grados, minutos y segundos se representan con símbolos como se muestran a continuación 64° 16´37´´ que se lee 64 grados 16 minutos y 37 segundos. Este sistema fue inventado por los babilonios, cuyas tablas de pesos y medidas estaban basadas en una escala de 60. Esto se debió probablemente a que ellos contaban el año de 360 días. Esto condujo a la división de la circunferencia de un círculo en 360°. Un radio trazado como cuerda subtiende entonces 60°, este grado se llama sexagesimal. Medida circular: en este sistema la unidad de medida es el radián, que es el
ángulo correspondiente a un arco cuya longitud es igual a la longitud del radio del círculo. En la figura se muestra que la longitud del arco AB es igual al radio del
círculo, por lo tanto: Ángulo AOB=1 radián La medida circular de un ángulo es su magnitud expresada en función de su radio y tiene la ventaja de que la longitud de un arco cualquiera tiene la misma medida en radios que el ángulo correspondiente en radianes. Relación entre estos dos sistemas. Por geometría sabemos que la longitud de una circunferencia es igual a 2 R lo que significa que

108
la razón de la circunferencia al radio es 2 , pero una circunferencia subtiende un
ángulo central de 360°; por lo tanto: 02 360 0
0 0
0 0 ´ "
180
180 1801 radián =
3.141593
1 radián 57.2958 57 17 44.8
De estas igualdades se deduce que:
00
0
0
3 180135
4
45180 4
rad
Obtén los grados o radianes según se requiera.
a) 0120 b)
2
c)
2
3
d) 0270
e) 0315
f) 3
2
g) 0150 h)
0300
i) 5
6
j)
6
k)
3
l)
4
Respuestas
a)2
3
b)090 c)
0120 d)
3
2
e) 7
4
f)0270
g) 5
6
h)
5
3
i) 0150 j)
030 k) 060 l)
045

109
ANGULOS ESPECIALES. Los cálculos de la trigonometría se basan en la relación que existe entre los lados y el ángulo agudo comprendido entre los lados de un triángulo rectángulo.
las 6 razones trigonometricas son:
sen
cos
tan
cot
sec
cos
co
hip
ca
hip
co
ca
ca
co
hip
ca
hip
co
El teorema de Pitágoras para los triángulos de 45 °, 30 ° y 60° nos permite obtener la relación de dichos ángulos con sus lados como se muestra en la siguiente tabla
Para los ángulos
sen
cos
tan
cot
sec
csc
600
3
2
1
2
33
1
1
3
22
1
2
3
450
1
2
1
2
1
1
22
1
22
1

110
300
1
2
3
2
1
3
33
1
2
3
22
1
Para poder construir las gráficas de las funciones trigonométricas se tiene que conocer el círculo unitario (circulo de radio =1)

111
Y algunas identidades trigonométricas las cuales nos ayudara a encontrar los valores.
tancos
sen
Ejemplo
00
0
30tan30 0.5773
cos30
sen
coscot
sen
Ejemplo
00
0
cos30cot 60 1.7320
30sen
1sec
cos
Ejemplo
0
0
1sec30 1.1547
cos30
1csc
sen
Ejemplo
0
0
1csc30 2
30sen
Con estos datos podemos llenar la siguiente tabla.
Ángulo rad sen cos tan cot sec csc 00 0 rad 0 1 0 1
030 1
6rad
0.5 0.8660 0.5773 1.7320 1.1547 2
045 1
4rad
0.7071 0.7071 1 1 1.4142 1.4142
060 2
6rad
0.8660 0.5 1.7320 0.5773 2 1.1547
090 1
2rad
1 0 0 1
0120 4
6rad
0.8660 0.5 1.7320 0.5773 2 1.1547
0135 3
4rad
0.7071 0.7071 1 1 1.4142 1.4142
0150 5
6rad
0.5 0.8660 0.5773 1.7320 1.1547 2
0180 rad
0 1 0 1
0210 7
6rad
0.5 0.8660 0.5773 1.7320 1.1547 2
0225 5
4rad
0.7071 0.7071 1 1 1.4142 1.4142
0240 8
6rad
0.8660 0.5 1.7320 0.5773 2 1.1547
0270 3
2rad
1 0 0 1
0300 10
6rad
0.8660 0.5 1.7320 0.5773 2 1.1547

112
0315 7
4rad
0.7071 0.7071 1 1 1.4142 1.4142
0330 11
6rad
0.5 0.8660 0.5773 1.7320 1.1547 2
0360 rad
0 1 0 1
GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS
Construyendo las gráficas de las funciones trigonométricas con los valores de los radianes (eje de x ) y el valor de sen, cos, tan, cot, sec y csc (eje de y ) para cada
una.
Función
Grafica
( ) ( )f x sen x
( ) cos( )f x x

113
( ) tan( )f x x
( ) cot( )f x x
( ) sec( )f x x
( ) csc( )f x x

114
Una vez revisadas las gráficas analizaremos los parámetros que modifican a las funciones sinusoidales que se definen como
( ) ( )
( ) cos( )
f x Asen bx c d
f x A bx c d
Donde : |A|: amplitud
b: frecuencia
c: desfasamiento o desplazamiento en el eje “x”
d: desfasamiento o desplazamiento en el eje “y”
El período de una función ( ) ( )f x Asen bx es el tamaño de la gráfica sobre el eje
de las abscisas donde inicia y termina dicha función. El periodo de la gráfica de una función empieza cuando el argumento es cero y termina cuando el argumento es igual a 2 .
El período puede calcularse con la siguiente fórmula: 2
pb
El primer parámetro es la amplitud |A|: nos indica que tan larga puede ser la
función.

115
El segundo parámetro es la frecuencia b: esta nos dice cuántos ciclos estarán en
el periodo de 2 rad como lo muestra la gráfica.
El tercer parámetro es c: el desfasamiento o desplazamiento en el eje de x , este
nos indica cuanto se desplazó horizontalmente.

116
El cuarto parámetro es el d: desfasamiento o desplazamiento en el eje “y”
Ejemplo 1. Determina la amplitud, período, frecuencia, dominio, rango y grafica de la siguiente
función ( ) 2 (3 )f x sen x
Calculando el periodo 2
3p
Amplitud: 2 Frecuencia: 3
Dominio y rango de la Función
:
: 2,2
f
f
D
R
20,
3p

117
Puedes comparar la función ( ) 2 (3 )f x sen x con ( ) 2 ( )f x sen x en donde se
observa que hay un ciclo cada 2
3
, la frecuencia indica que hay tres ciclos cada
2 .
Ejemplo 2.
Considera la función ( ) 3cos 22
h x x
para encontrar amplitud, periodo,
dominio y rango así como el desfasamiento horizontal. Para calcular el periodo también puedes plantearlo como una ecuación. Para el inicio y fin del ciclo
0
0
2 0 2 22 2
2 2 2 2 2
32 2 2 2
3
2 4 2
f
x x
x x
x x
x x
3
4fx

118
Realizando los cálculos obtenemos que el periodo es:
3: ,
4 4p
Amplitud: 3 Dominio y rango de la Función
:
: 3,3
f
f
D
R
. Ejemplo 3. Las temperatura Fahrenheit normal mensual es Alburquerque, NM, se puede observar en la siguiente tabla (mes 1=enero, 2=febrero y así sucesivamente).
Modele la temperatura (t) como una función sinusoidal del tiempo, usando 36 como valor mínimo y 79 como valor máximo .Respalde su respuesta gráficamente.
Para calcular la amplitud A se tiene que sacar un valor medio entre la
temperatura mayor y la menor.
2
mayor menort tA
79 3621.5
2A
Para calcular el desplazamiento vertical sólo tendremos que una diferencia.
mayord t A 79 21.5 57.5d
menord t A 36 21.5 57.5d
Calculando el periodo:
0fp x x 12 1
11
p
p
Para calcular la frecuencia de la función es:
2p
b
211
b
Despejando a
2
11b
Para calcular el desfasamiento o desplazamiento en el eje “x”
Sabemos que 0bx c de donde c
xb
sustituimos los valores 1
2
11
c
el valor
de 2
11c
Mes 1 2 3 4 5 6 7 8 9 10 11 12
temp. 36 41 48 56 65 75 79 76 69 57 44 36

119
La función obtenida es:
2 2( ) 21.5cos 57.5
11 11f x x
Y la gráfica que nos representa dicha función es la siguiente.
36,79
f
f
D
R
Ejercicios.
Obtén la amplitud, desfasamiento vertical el periodo, fD , fR , y gráfica de las
siguientes funciones:
) ( ) 3cos(2 )
) ( ) 2 24
) ( ) 3 32
) ( ) cos(2 3 )
) ( ) 5 2 36
a f x x
b f x sen
c f x sen x
d f x x
e f x sen x
1) ( ) 2cos 6
6
1 1) ( ) cos 2 1
2 3
3) ( ) 2 2 3
4
2) ( ) 2
3
) ( ) 3cos( ) 4
f f x x
g f x x
h f x sen x
i f x sen x
j f x x

120
Respuestas
a) Amplitud A=3
,2 2
3,3
f
f
P
D
R
Desfasamiento vertical d=0
b) Amplitud A=2
8 ,0
2,2
f
f
P
D
R
Desfasamiento vertical d=0
c) Amplitud A=3
5,
6 6
3,3
f
f
P
D
R
Desfasamiento vertical d=0
d) Amplitud A=1
3 5,
2 2
1,1
f
f
P
D
R
Desfasamiento vertical d=0
e) Amplitud A=5
11,
12 12
2,8
f
f
P
D
R
Desfasamiento vertical d=3
f) Amplitud A=2
11,
6 6
8, 4
f
f
P
D
R
Desfasamiento vertical d=-6
g)
Amplitud A=1
2
5,
6 6
1 3,
2 2
f
f
P
D
R
Desfasamiento vertical d=1
h) Amplitud A=2
3 11,
8 8
5, 1
f
f
P
D
R
Desfasamiento vertical d=-3

121
i) Amplitud A=1
2 8,
6 6
1 3,
2 2
f
f
P
D
R
Desfasamiento vertical d=0
J) Amplitud A=3
0,2
1,7
f
f
P
D
R
Desfasamiento vertical d=0
Problemas de aplicación 1.-Una hoja flota sobre el agua balanceándose hacia arriba y hacia abajo. La distancia entre su punto alto y el más bajo es de 4 cm. La hoja se mueve desde su punto más alto hacia abajo y de regreso a su punto superior cada 10 segundos. Escribe una función coseno que represente el movimiento de la hoja en relación con el punto de equilibrio. 2.-Escriba una función seno que represente la oscilación de las mareas en Savannah, Georgina, si el punto de equilibrio es de 4.24pies, la amplitud es 3.55 pies, el desplazamiento de fase es -4.68horas y el periodo es 12.40 horas. 3.-Un peso de 3kg cuelga al final de un resorte que se estira 2cm debajo de la posición de equilibrio. Despreciando la resistencia del aire y la fricción, la distancia y que el peso se desplaza con respecto a la posición de equilibrio en un tiempo t
segundos está dada por ( ) 3cos(8 )f x t Exprese el periodo P y la amplitud A del
peso que cuelga, y grafíquela para 0 t .
4.-Un adulto normal sentado aspira y exhala cerca de 0.820 litros de aire cada 4 segundos. El volumen de aire en los pulmones después de t segundos que
exhala es aproximadamente ( ) 0.46 0.36cos2
v t t
. Grafique la función exhala –
inhala indicad. ¿Al exhalar, los pulmones se quedan sin aire? Si no es así ¿Qué volumen queda de remanente? 5.-La cantidad de bióxido de azufre, obtenido de la combustión de combustible liberado hacia la atmósfera de una ciudad varía estacionariamente. Suponga que el número de toneladas de contaminantes liberado en la atmósfera durante cualquier semana después del primero de enero para cierta ciudad está dado por:
( ) cos 1.526
nA n
donde 0 104n
Grafique la función en el intervalo indicado y describa lo que muestra la gráfica.

122
Respuesta Problemas de aplicación Ejercicio 1
2A
0d
10p
0c
( ) 2cos5
f x x
Ejercicio 2
3.55A
4.24d
12.4p
2.37c
( ) 3.55 (.506 2.27) 4.24f x sen x
Ejercicio 3
A 3
8b
0,4
p
( ) 3cos(8 )f x x

123
Ejercicio 4
Al exhalar los pulmones no quedan sin aire y el volumen
queda ( ) 0.1 ltsV x
Ejercicio 5
1A
26b
1.5d
0c
0,52p

124
Bibliografía
Arya, Jagdish C. - Lardner, Robín. Matemáticas aplicadas a la administración y a
la economía. Prentice Hall. México, 2009.
Swokowski-Cole. Álgebra y trigonometría con geometría analítica. 12ª Edición,
CENGAGE Learning. México, 2009.
Sobel, M. (1998). Pre cálculo. México. Prentice Hall.
Barnett R. (2000). Pre cálculo. México. Mc Graw-Hill.
Leithold, L. Algebra y Trigonometría con Geometría analítica. México: Oxford
University Press.
Barnett, R., Zeegler, M. y Byleen, K. (2000). Algebra, México: Mc. Graw Hill.