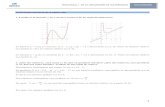
Extremos Relativos y Monotonía

@ Angel Prieto Benito Matemáticas Acceso a CFGS 1

EXTREMOS RELATIVOSy

CRECIMIENTO

Bloque III * Tema 124


• INTERVALO Y ENTORNO

• Sea un intervalo cerrado [a, b] en R.• Representa el conjunto de valores tales que a ≤ x ≤ b• Sea un intervalo abierto (a, b) en R.• Representa el conjunto de valores tales que a < x < b

• Sea el entorno cerrado E[a, r] en R.• Representa el conjunto de valores tales que (a – r) ≤ x ≤ (a + r)• Sea el entorno abierto E(a, r) en R.• Representa el conjunto de valores tales que (a – r) < x < (a + r)

• El intervalo [-2, 2] representa lo mismo que el entorno E[0, 2].• El intervalo (-1, 5] representa lo mismo que el entorno E(2, 3).• Cuando lo que interesa de una función es su comportamiento en las

cercanías de un punto de su dominio se emplea el entorno.

ENTORNO DE UN PUNTO


• CRECIMIENTO Y DECRECIMIENTO

• Sea una función f(x) definida en el entorno de un punto x=a.• f(x) es creciente en x=a si existe un entorno de a para el que se cumple:• f(a) < f(x) en todo punto x de dicho entorno situado a la derecha de a (x < a).• f(a) > f(x) en todo punto x de dicho entorno situado a la izquierda de a (x > a).

• f(x) es decreciente en x=a si existe un entorno de a para el que se cumple:• f(a) > f(x) en todo punto x de dicho entorno situado a la derecha de a (x < a).• f(a) < f(x) en todo punto x de dicho entorno situado a la izquierda de a (x > a).• • EXTREMOS RELATIVOS

• f(x) tiene un máximo relativo en x=a si existe un entorno de a para el que se cumple • f(a) ≥ f(x).• f(x) tiene un mínimo relativo en x=a si existe un entorno de a para el que se cumple • f(a) ≤ f(x)

EXTREMOS RELATIVOS


Gráfico

0 a-r a a+r b-r b b+r

f(a+r)f(a)f(a-r)

f(b-r)

f(b)

f(b+r)

En x=a la función es creciente

En x=b la función es decreciente


Gráfico


f(a)f(a-r)f(a+r)

f(b-r)=f(b+r)f(b)

En x=a la función tiene un máximo relativo.

En x=b la función tiene un mínimo relativo

Max(a,f(a))

Min(b,f(b))


• CRECIMIENTO Y DECRECIMIENTO

• Si una función es creciente en un entorno de un punto x=a, la recta tangente en el punto (a, f(a)) presenta una pendiente positiva.

• Conclusión:• Si f ’(a) > 0 entonces en x=a la función es creciente.

• Si una función es decreciente en un entorno de un punto x=a, la recta tangente en el punto (a, f(a)) presenta una pendiente negativa.

• Conclusión:• Si f ’(a) < 0 entonces en x=a la función es decreciente.

• EXTREMOS RELATIVOS

• Si una función presenta un máximo o un mínimo relativo en un entorno de un punto x=a, la recta tangente en el punto (a, f(a)) presenta una pendiente nula (m=0).

• Conclusión:• Si f ’(a) = 0 entonces en x=a la función presenta un máximo o un mínimo relativo.

EXTREMOS Y DERIVADAS


Gráfico


f(a+r)f(a)f(a-r)

f(b-r)

f(b)

f(b+r)

En x=a la función es creciente

En x=b la función es decreciente


Gráfico


f(a)f(a-r)f(a+r)

f(b-r)=f(b+r)f(b)

En x=a la función tiene un máximo relativo.

En x=b la función tiene un mínimo relativo

Max(a,f(a))

Min(b,f(b))


• EJEMPLO 1

• Hallar los máximos y mínimos relativos de la función:• y = 2.x3 + 3.x2 – 12.x – 5

• Hallamos su derivada: y ‘ = 6.x2 + 6.x – 12• La igualamos a cero: 6.x2 + 6.x – 12 = 0• Simplificamos: x2 + x – 2 =0• Resolvemos la ecuación: x = - 2 y x = 1

• En x = -2 habrá un máximo o un mínimo relativo.• En x = 1 habrá un máximo o un mínimo relativo.• Normalmente si en uno de los puntos hay un máximo en el otro hay un

mínimo.• Para determinar si es máximo o mínimo estudiaremos su entorno.

Ejemplos


- 3 -2 -1 0 1 2

• Teníamos la función:

• y = 2.x3 + 3.x2 – 12.x – 5

• En x=1

• f(1)= 2 + 3 – 12 – 5 = - 12• f(0,9) = 2.0,93 + 3.0,92 – 12.0,9 – 5 =• = - 11,92• f(1,1) = 2.1,13 + 3.1,12 – 12.1,1 – 5 =• = - 11,908• Luego en x=1 hay un MÍNIMO RELATIVO

• En x= - 2

• F(-2)= - 16 + 12 + 24 – 5 = 36 – 21 = 15

• f(-1,9) = - 2.1,93 + 3.1,92 + 12.1,9 – 5 = 14,912• f(-2,1) = 2.(-2,1)3 + 3.(-2,1)2 – 12.(-2,1) – 5 = 14,908• Luego en x=-2 hay un MÁXIMO RELATIVO

Mín(1, - 12)

Máx(-2, 15)


• EJEMPLO 2

• Sea la función, ya empleada: y = 2.x3 + 3.x2 – 12.x – 5

• Hallamos su derivada: y ‘ = 6.x2 + 6.x – 12• Simplificamos: y ‘ = 6.(x2 + x – 2 )• Resolvemos la ecuación: x = - 2 y x = 1 son las raíces de y ‘• Factorizamos: y ‘ = 6.( x + 2).(x – 1)• Los intervalos a estudiar son:• (-oo, -2) , (-2, 1) y (1, +oo) • En ( - oo, -2) y ` > 0 Pendiente positiva Función Creciente.• En ( - 2, 1) y ` < 0 Pendiente negativa Función Decreciente.• En ( 1, + oo) y ` > 0 Pendiente positiva Función Creciente.

Ejemplos


• EJEMPLO 3

• Sea la función: y = x / (x – 1)• Determinar los intervalos de crecimiento y decrecimiento.

• En x = 1 la función presenta una asíntota vertical.• Hallamos su derivada: y ‘ = [1.(x – 1)– 1.x] / (x – 1)2

• Simplificamos: y ‘ = - 1 / (x – 1)2 • Como y’ no puede ser 0, la función no presenta máx. ni mín.• Intervalos:• • En ( - oo, 1) y ` (0) = - 1 < 0 Pendiente negativa Decreciente.• En ( 1, + oo) y `(2) = -1 < 0 Pendiente negativa Decreciente.

Ejemplos


• EJEMPLO 4

• Sea la función: y = 2 / (x2 – 4)• Determinar los intervalos de crecimiento y decrecimiento.

• En x = -2 y en x=2 la función presenta asíntotas verticales.• Hallamos su derivada: y ‘ = [0.(x2 – 4)– 2.2x] / (x2 – 4)2

• Simplificamos: y ‘ = - 4x / (x2 – 4)2 • Hacemos y’ = 0 x = 0• En x = 0 la función presenta un máximo o un mínimo.• Intervalos:• En ( - oo, -2) y ` (-3) = > 0 Pendiente positiva Creciente.• En ( -2, 0) y ` (-1) = > 0 Pendiente positiva Creciente.• En ( 0, 2) y ` (1) = < 0 Pendiente negativa Decreciente.• En ( 2, + oo) y ` (3) = < 0 Pendiente negativa Decreciente.

Ejemplos


• Si en lugar de pedirnos la derivada de la función en x = a, nos dan dicho valor y nos piden la abscisa, se procede así:

• Se halla la expresión f ’(x)• Se resuelve la ecuación f ’(x) = k

• EJEMPLO

• Sea la función, ya empleada: y = 2.x3 + 3.x2 – 12.x – 5• ¿Para qué valor de x la pendiente de la recta tangente valdrá m=2?

• Hallamos su derivada: y ‘ = 6.x2 + 6.x – 12• Resolvemos la ecuación: 2 = 6.x2 + 6.x – 12 6.x2 + 6.x – 14 = 0 3.x2 + 3.x – 7 = 0 x = [ - 3 +/- √(9 + 84)] / 6 = 1,11 y - 2,11

• En x = -2,11 y en x = 1,11 la pendiente de la tangente vale m=2.

Obtención de abscisas para f ‘(x)=k


• EJEMPLO

• Hallar el valor de a para que el máximo de la función• y = – 2 .x2 + 4.x + a valga 8.

• Derivamos e igualamos a cero, pues al ser un máximo su pendiente es nula.• y`= - 4x + 4 = 0 x = 1 es la abscisa donde está el máximo.• 8 = – 2 .12 + 4.1 + a a = 8 + 2 – 4 a = 6

• EJEMPLO

• Hallar el valor de a y b para que la función• y = x3 + a.x2 + b.x + 1 tenga un mínimo en el punto P(2, - 15)

• Derivamos e igualamos a cero, pues al ser un mínimo su pendiente es nula.• y`= 3.x2 + 2.a.x +b = 0 x = 2 es una de las dos soluciones.• 12+4.a+b = 0 b = – 4.a – 12 se debe cumplir.• Sustituyendo en la función: – 15 = 23 + a.22 + (– 4.a – 12).2 + 1 • – 15 = 8 + 4.a – 8.a – 24 + 1 4.a = 0 a = 0 b = – 12

Extremos Relativos y Monotonía

Documents

Transcript of Extremos Relativos y Monotonía