Complejidad Computacional del Metodo Simplex

y Metodos de Puntos Interiores*

Omar Trejo - 119711

Octubre, 2013

1. Tiempo Exponencial

La idea general del metodo Simplex para resolver problemas de programa-cion lineal es recorrer las aristas, vertice por vertice, de un polıtopo (regionfactible) revisando su optimalidad en cada paso. La cantidad maxima de verti-ces dados por el sistema Ax ≤ b (que define el polıtopo del problema), dondeA ∈ Rmxn, es

(nm

), aunque cotidianamente se prueba un numero menor que este.

Sin embargo, el hecho de que la cantidad de pruebas necesarias este relacionadaa una expresion combinatoria indica un posible problema con la complejidadcomputacional del algoritmo.

1.1. Problema Klee-Minty

El ejemplo utilizado cotidianamente para demostrar la complejidad exponen-cial del metodo Simplex es el problema Klee-Minty. La idea basica es deformarun hipercubo de tal manera que el metodo deba recorrer todas las aristas antesde llegar al punto optimo. Inicialmente fue propuesto en 1972 por Klee y Mintycon la forma

maximizarx

yn

s.a. εyj−1 ≤ yj ≤ 1− εyj−1, j = 2, . . . , n,

yj ≥ 0, j = 1, . . . , n.

Poco despues Chvatal propuso[3] el cambio de variable x1 = y1, xj =(−1/ε)yj−1 + yj , lo que permite formular el problema como es mas popular-

*Este documento no contiene un tratado riguroso de los metodos. Se crea a manera deresumen y se omiten muchos detalles tecnicos.

1

Figura 1: Politopos de Klee-Minty de dos y tres dimensiones[4].

mente conocido,

maximizarx

n∑k=1

10n−kxk

s.a. 2

j−1∑k=1

10j−kxk + xj ≤ 100j−1, j = 1, . . . , n,

xj ≥ 0, j = 1, . . . , n.

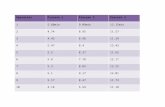
Los resultados del problema Klee-Minty, utilizando el algoritmo programadoy mostrado en la seccion Codigo, son

Dimensiones Iteraciones

3 505 476 318 3510 45

Esto claramente muestra la complejidad exponencial del metodo. Por lo mis-mo, muchos de los esfuerzos comenzaron a enfocarse en metodos de puntosinteriores, los cuales exhibıan caracterısticas deseables como complejidad poli-nomial.

2. Metodos de Puntos Interiores

Los metodos de puntos interiores han sido foco de atencion desde que semostro que existen problemas de complejidad exponencial para el metodo Sim-plex, y existe una variedad estos.1 En esta seccion explicaremos brevemente el

1Un contraste interesante es que el metodo Simplex genera su complejidad del numero derestricciones que presenta el problema, mientras que los metodos de puntos interiores generan

2

metodo elipsoidal y el metodo primal-dual infalible, y dejaremos de lado losdemas por cuestiones de espacio. La tabla[4] presentada continuacion resume lainformacion.

Ano Metodo Autor Caracterıstica

1947 Simplex Dantzig Eficiente en la practica1979 Elipsoidal Khachiyan Ineficiente en la practica1990 Primal-Dual Kojima, Mizuno, Yoshise Metodo Dominante

Infactible

2.1. Metodo Elipsoidal de Khachiyan

2.1.1. ¿En que consiste?

La idea basica del metodo elipsoidal se deriva de investigaciones previas,durante los anos sesenta y setenta, dentro de lo que era la Union Sovietica.De manera burda, la idea es encerrar la region de interes en una sucesion deelipsoides que decrecen de tamano cada vez mas. La contribucion de Khachiyanfue demostrar en sus dos publicaciones -publicadas en 1979 y 1980- que bajociertas condiciones el metodo tiene complejidad polinomial para problemas deprogramacion lineal.

2.1.2. ¿Como se construye el punto inicial y la sucesion de elipsoi-des?

El metodo construye una elipsoide inicial que cubre P , el conjunto de fac-tibilidad, completamente. Se toma el centro de ese elipsoide y se identifica sise encuentra dentro de la region factible P . Si se encuentra dentro, el proble-ma es factible, si no se encuentra dentro se puede construir un elipsoide nuevo(en tiempo polinomial), tomando en cuenta la variable que corresponde a larestriccion de ATx ≤ b que es violada, que cubra completamente la mitad delelipsoide anterior del lado donde se encuentra P . Procedemos de esta manerahasta que se encuentra un centro dentro de la region factible, o se alcanza elnumero maximo de iteraciones disponibles (el resultado en este caso serıa queel problema es no factible).

2.1.3. ¿Por que es un metodo polinomial?

Bajo dos condiciones, que explicaremos a continuacion, Bertismas y Tsitsiklismostraron[5] que el metodo elipsoidal resuelve problemas de programacion linealen tiempo O(m4 log(R/r)). Antes de definir las condiciones debemos definir elconjunto poliedrico del problema (representacion del problema de programacionlineal de manera vectorial):

P = {x ∈ Rm : aTj x ≤ cj , j = 1, . . . , n}

su complejidad debido al numero de variables en el problema.

3

Figura 2: Elipsoides con y sin region factible[8].

Si P 6= ∅ el problema tiene solucion. Las dos condiciones para que el algoritmoconverja en tiempo polinomial son:

1. ∃ x0 ∈ Rm, ∃ r ∈ R, r > 0, t.q. P ⊂ S(x0,R) = {x ∈ Rm : ‖x− x0‖ ≤ R},

2. ∃ r ∈ R, r > 0 conocido t.q. si Y 6= ∅ =⇒ S(x∗, r) ⊂ Y,

donde S(y, r) es una bola con centro en y y radio r. La primer condicionimplica que P esta acotado. La segunda condicion implica que si P es no vacıo,entonces su interior tampoco es vacıo; i.e. existe un sentido de densidad.

Dado que tenemos un sentido de densidad, podemos construir cualquier elip-soide necesaria. La parte computacionalmente mas compleja del metodo es preci-samente la construccion del elipsoide de volumen mınimo. Sin embargo, sabemosque este proceso es de complejidad polinomial, por lo que, de manera burda,podemos extender esto al hecho de que el metodo es de complejidad polinomial.En la teorıa se pueden construir (con aritmetica exacta) sucesiones infinitas deelipsoides, pero en la practica (aritmetica de precision finita) se establece unacota al numero de iteraciones que si es superada el problema se considera queeste es infactible.

2.1.4. ¿Cual es la relevancia teorica del metodo y por que no espractica su implementacion para programacion lineal?

La relevancia teorica del metodo reside en el hecho de que antes de la publi-cacion del mismo no se habıan logrado clasificar los problemas de programacionlineal en alguno de los conjuntos de problemas P o NP, i.e. los que se puedenresolver en tiempo polinomial y los que no, respectivamente. Se creıa que es-tos problemas no tienen una complejidad tal que deben ser clasificados en NP,pero nadie habıa conseguido demostrar su pertenencia a P hasta que Kachiyanpublico su metodo elipsoidal. Ademas el metodo sirve para construir algorit-mos para problemas de optimizacion convexa, que son mas generales que los deprogramacion lineal.

4

La experiencia computacional muestra que las iteraciones necesarias pararesolver problemas de programacion lineal usando este metodo se encuentranmuy cercanas al lımite teorico superior. Esto significa que practicamente el al-goritmo no es muy bueno. El metodo Simplex, aunque tiene una complejidadexponencial, en la practica la experiencia muestra que son necesarias muchasmenos iteraciones que el lımite teorico maximo, haciendolo un candidato paraaplicaciones practicas.

2.2. Metodo Primal-Dual Infactible de Kojima, Mizuno &Yoshie

2.2.1. ¿En que consiste?

El metodo consiste en tomar un punto nuevo en cada iteracion a lo largode la direccion de Newton, en la direccion de la trayectoria central, como lohacen otros metodos de puntos interiores. La diferencia es que este metodo norequiere que los puntos esten dentro de la region factible. Este metodo aplicapasos largos y distintos entre el los problemas primal y dual, y se caracterizapor convergencia global en tiempo polinomial2

2.2.2. ¿Como se construye el punto inicial y la sucesion de puntos?

Dado que es un metodo infactible, tenemos que no es necesario construir unpunto inicial, i.e. cualquier punto (xi, yi, zi) en el espacio, con xi ≥ 0, zi ≥ 0,convergera eventualmente a una solucion. Es necesario notar que hay casos enprogramacion no-lineal donde esta solucion puede ser no-optima, pero en el casode programacion lineal, siempre convergera a una solucion optima.

La sucesion de puntos se construye utilizando los problemas primal y dual

P : minimizarx

cTx

s.a. Ax = b, x ≥ 0

D : maximizary,z

bT y

s.a. AT y + z = c, z ≥ 0

En cada iteracion se resuelve el sistema A 0 00 AT IZk 0 Xk

∆x∆y∆z

= −

Axk − bAT yk + zk − cXkZk − µe

donde Zk y Xk son las matrices con la diagonal igual a zk y xk, respecti-

vamente. Cada una de las restricciones (ecuaciones del sistema lineal) vienen

2Para ser rigurosos deberıamos definir los conceptos direccion de Newton, trayectoria cen-tral, pasos largos, problema primal y problema dual. Sin embargo, por cuestiones de espaciono profundizaremos en ellos.

5

de la busqueda de cerar la brecha en la restriccion de factibilidad de P , la res-triccion de factibilidad de D y la restriccion de la brecha entre los problemas,XkZk = µe, respectivamente. Posteriormente se actualizan las variables

(xk+1, yk+1, zk+1) = (xk, yk, zk) + α(∆x,∆y,∆z)

Los detalles tecnicos, por ejemplo como escoger α en cada iteracion, la ob-tencion de la factibilidad, la convergencia global o la identificacion de la no-factibilidad, no seran explicados en este documento. Sin embargo, esto no sig-nifica que carezcan de gran importancia.

2.2.3. ¿Por que es un metodo polinomial?

Aunque el calculo de cada iteracion es significativamente mas alto que elmetodo Simplex, cada iteracion conlleva progreso mucho mas significativo haciael optimo, suponiendo que existe. Ademas es un camino mucho mas directo (si-gue el llamado central path). La complejidad del algoritmo radica en la solucionde un sistema de ecuaciones lineales que, aunque puede ser complicado, sabe-mos que podemos hacer en tiempo polinomial, por lo que el algoritmo tambienmuestra tiempo polinomial3.

2.2.4. ¿Cual es la relevancia del metodo y por que es practica suimplementacion para programacion lineal?

El metodo se encuentra dentro de los mas populares hoy en dıa y exhibelos mejores resultados practicos. En promedio le toma entre 23 y 25 iteracionesresolver los problemas mas complejos (con solucion) que existen hoy en dıa enprogramacion lineal. Ademas, teoricamente es importante el metodo porque nose restringe a comenzar con puntos dentro de la region factible, lo que puedepresentar un problema en sı mismo.

3. Codigo - Metodo Simplex Revisado

El codigo aquı presentado es una pequena variacion del metodo Simplex queutiliza un tableu mas pequeno porque no guarda espacio para las columnas Bde A = [N |B] que contienen la identidad en cada iteracion. En realidad noes necesario almacenar esta identidad. La utilizacion de este metodo es paramejorar el desempeno en el RAM de la computadora4.

/** Programacion Lineal - Metodo Simplex Revisado

* Omar Trejo Navarro

* 119711

*

3Claramente esta es una implicacion burda y es necesario sustentarla de manera rigurosa,pero dicha prueba no sera presentada en este texto.

4Para los problemas pedagogicos que resolveremos en clase este detalle es intrascendente.

6

* r := y = maximizar, n = minimizar

* nv := numero de variables de funcion objetivo

* nr := numero de restricciones

* t := tableu

* tipo := 1 = maximizar, -1 = minimizar

* ai := auxiliar para inputs

* optimo := true = alcanzado, false = no alcanzado

* xmax := maximo de coeficientes de funcion objetivo

* bamin := mininmo de b_i/a_ij

* aux := variable auxiliar

* rp := indice del renglon pivote

* cp := indice de la columna pivote

* error := true = no acotado, false = acotado

* CMAX := maxima cantidad de restricciones

* VMAX := maxima cantidad de variables

**/

#include <stdio.h>#include <math.h>

#define CMAX 10#define VMAX 10

int nr, nv, rp, cp;bool optimo, error;double t[CMAX][VMAX];

void datos() {/** Obtener los datos del problema

*/char r;int i, j;double tipo, ai;printf("\n Programacion Lineal - Metodo Simplex Revisado\n");do {

printf("\n Maximizar [s/n] ? ");scanf("%c", &r);if (r == 'S' || r == 's')

tipo = 1;else if (r == 'N' || r == 'n')

tipo = -1;else

printf("\n [!] Error. Debe indicar si (s) o no (n).\n\n")←↩;

} while (r != 'S' && r != 's' && r != 'N' && r != 'n');printf(" Cantidad de variables ? "); scanf("%d", &nv);printf(" Cantidad de restricciones ? "); scanf("%d", &nr);// Funcion objetivoprintf("\n Funcion objetivo:\n");for (j = 1; j <= nv; j++) {

printf(" Coeficiente de la variable %d ? ", j);scanf("%lf", &ai);t[1][j + 1] = ai * tipo;

}printf(" Valor de la constante ? ");

7

scanf("%lf", &ai);t[1][1] = ai * tipo;// Restriccionesfor (i = 1; i <= nr; i++) {

printf("\n Restriccion %d:\n", i);for (j = 1; j <= nv; j++) {

printf(" Coeficiente de la variable %d ? ", j);scanf("%lf", &ai);t[i + 1][j + 1] = -ai;

}printf(" Constante de restriccion ? ");scanf("%lf", &t[i + 1][1]);

}// Indices de las variablesfor (j = 1; j <= nv; j++)

t[0][j + 1] = j;for (i = nv + 1; i <= nv + nr; i++)

t[i - nv + 1][0] = i;}

void pivotear() {/** Hacer el cambio de pivotear

*/double bamin, aux, xmax;int i, j;xmax = 0;// maximo {costos reducidos}for (j = 2; j <= nv + 1; j++) {

if (t[1][j] > 0 && t[1][j] > xmax) {xmax = t[1][j];cp = j;

}}bamin = 1000000;// minimo {b_i/a_ij}for (i = 2; i <= nr + 1; i++) {

if (t[i][cp] < 0) {aux = fabs(t[i][1] / t[i][cp]);if (aux < bamin) {

bamin = aux;rp = i;

}}

}// Cambio de indicesaux = t[0][cp];t[0][cp] = t[rp][0];t[rp][0] = aux;

}

void actualizar() {/** Actualizar el tableu

*/int i, j;for (i = 1; i <= nr + 1; i++)

8

if (i != rp)for (j = 1; j <= nv + 1; j++)

if (j != cp)t[i][j] -= t[rp][j] * t[i][cp] / t[rp][cp];

t[rp][cp] = 1.0 / t[rp][cp];for (j = 1; j <= nv + 1; j++)

if (j != cp)t[rp][j] *= fabs(t[rp][cp]);

for (i = 1; i <= nr + 1; i++)if (i != rp)

t[i][cp] *= t[rp][cp];}

void revisar() {/** Revisar optimalidad del tableu

*/int i, j;optimo = true;error = false;// Revisar si es no-acotadofor (i = 2; i <= nr + 1; i++)

if (t[i][1] < 0)// TODO: Avisar que es no acotadoerror = true;

// Revisar si es optimoif (error == false)

for (j = 2; j <= nv + 1; j++)// TODO: Revisar si hay solucion multipleif (t[1][j] > 0)

optimo = false;}

void simplex() {/** Metodo Simplex Revisado

*/while (optimo == false) {

pivotear();actualizar();revisar();

}}

void resultados() {/** Presentar los resultados

*/int i, j;printf("\n Resultados:\n");if (error == false) {

for (i = 1; i <= nv; i++)for (j = 2; j <= nr + 1; j++)

if (t[j][0] == 1 * i)printf(" Variable %d: %f\n", i, t[j][1]);

printf(" Funcion objetivo: %f\n\n", t[1][1]);} else

9

printf(" No hay solucion.\n\n");}

int main() {datos();simplex();resultados();

}

Referencias

[1] Stephen J. Wright, Primal-Dual Interior Point Methods, Argonne NationalLaboratory, SIAM, 1997.

[2] Mokhtar S. Bazaraa, John J. Jarvis, Hanif D. Sherali, Linear Programmingand Network Flows, Wiley, 2010.

[3] Steven R. Dunbar, Worst Case and Average Case Behavior of the SimplexAlgorithm, University of Nebraska-Lincoln, Department of Mathematics.

[4] A. Deza, E. Nematollahi & T. Terlaky, How good are interior point methods?,McMaster University, Advanced Optimization Laboratory, 2005.

[5] Yinyu Ye, The Ellipsoid (Kachiyan) Method, Department of ManagementScience and Engineering, Stanford University.

[6] Robert G. Bland, Donald Goldfarb & Michael J. Todd The Ellipsoid Method:A Survey, Cornell University, Ithaca, New York, 1981.

[7] Masakazu Kojima, Nimrod Megiddo & Shinji Mizuno A primal-dual infeasi-ble interior point algorithm for linear programming, Mathematical Program-ming, North-Holland, 1992.

[8] Steffen Rebennack Ellipsoid Method, Encyclopedia of Optimization, Sprin-ger, 2008.

10