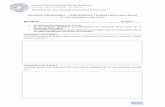
Modelado de sistemas físicos - cartagena99.com · Modelado de sistemas ... y secundario del...
Transcript of Modelado de sistemas físicos - cartagena99.com · Modelado de sistemas ... y secundario del...
4–1
4 Modelado de sistemas
físicos
En el capítulo anterior se presentó el concepto de función de transferencia como una forma alternativa de modelado de sistemas LTI frente a la ecuación diferencial lineal de coeficientes constantes. Se trata de un modelo matemático compacto que permite deducir fácilmente las propiedades del sistema modelado. Además, mediante un diagrama de bloques es posible abordar el modelado de sistemas complejos compuestos de subsistemas interconectados con funciones de transferencia conocidas.
En este capítulo se describirán diferentes procedimientos para obtener la función de transferencia de un sistema físico siempre que se pueda hacer la suposición de que su respuesta es lineal e invariante en el tiempo. Estas técnicas de modelado se pueden aplicar a todo tipo de sistemas independientemente de su naturaleza. En este capítulo se ilustrarán dichas técnicas en circuitos eléctricos y electrónicos, sistemas mecánicos de traslación y rotación, sistemas térmicos y sistemas de conducción de fluidos compuestos por depósitos y tuberías. En todos los ejemplos de este capítulo, la notación habitual será utilizar minúsculas para las variables dependientes del tiempo y mayúsculas para sus transformadas de Laplace.
4.1 Circuitos eléctricos En esta sección no se pretende dar un curso completo sobre circuitos eléctricos, ya que se supone que el alumno ha aprendido estos conocimientos en un curso previo. Se trata simplemente de aplicar los conceptos adquiridos para poder calcular funciones de transferencia entre diferentes magnitudes del circuito. A modo de breve resumen, se exponen a continuación los conceptos fundamentales para este curso. Un circuito eléctrico se define como un conjunto de componentes eléctricos interconectados que contiene al menos una trayectoria cerrada por la que pueda fluir una corriente eléctrica. Se llama malla en un circuito a cualquier trayectoria cerrada que podamos definir en él. Una rama representa cualquier elemento de dos terminales dentro de un circuito. El contorno de cada malla está formado por ramas. Se llama nudo a cualquier punto de conexión en el que concurren dos o más ramas. Por las ramas circulan corrientes eléctricas y cada nudo tiene su propia tensión eléctrica.
4–2
Los componentes eléctricos que constituyen un circuito pueden ser activos (aportan o consumen energía) o pasivos (disipan energía en forma de calor o la almacenan). Entre los elementos activos están las fuentes de alimentación, ya sean independientes o dependientes de alguna otra variable eléctrica del circuito. Entre los elementos pasivos se consideran las resistencias, las bobinas y los condensadores. Además de estos elementos activos y pasivos, también pueden aparecer transformadores ideales. Estos transfieren íntegramente la potencia eléctrica entre diferentes partes de un circuito, transformando las tensiones y las corrientes entre los arrollamientos primario y secundario del transformador según su relación de transformación.
La corriente de cada rama y las tensiones de los nudos terminales de la misma guardan una relación matemática que depende de los componentes presentes en dicha rama. La resolución de un circuito consiste en la determinación de las corrientes de todas sus ramas y de las tensiones de todos sus nudos. Para ello se utiliza la denominada teoría de circuitos que consiste en un conjunto de leyes que relacionan las tensiones de los nudos y las corrientes de las ramas en función de la topología del circuito. Entre los fundamentos teóricos especialmente útiles en este contexto y que debería conocer el alumno se pueden citar: la ley de Ohm, el cálculo de resistencias equivalentes para conjuntos de resistencias interconectadas en serie y/o paralelo, la primera y segunda ley de Kirchoff, los teoremas de Thèvenin y Norton, el principio de superposición y la resolución de divisores de tensión y corriente. El objetivo en este capítulo es poder obtener cualquier función de transferencia en un circuito, donde la entrada será la tensión o corriente de una fuente independiente y la salida cualquier corriente de rama, tensión de nudo o diferencia de tensiones entre nudos. Como primer paso para alcanzar este objetivo, es necesario introducir el concepto de impedancia operacional Z(s) de un componente pasivo (resistencia, bobina o condensador) como el cociente entre la transformada de Laplace de la diferencia de tensión entre sus terminales V(s) y la transformada de Laplace de la corriente I(s) en ausencia de condiciones iniciales.
nulasicsIsVsZ
..)()()( ⎟⎟⎠
⎞=
A continuación se presentan las relaciones entre la diferencia de tensión entre terminales y la corriente, así como la impedancia operacional resultante, para cada uno de los componentes pasivos que pueden aparecer en un circuito.
• Resistencia: componente pasivo que disipa energía en forma de calor por efecto Joule. La relación entre la diferencia de tensión en sus terminales v(t) y la corriente que circula por la resistencia i(t) viene dada por la ley de Ohm. La constante de proporcionalidad ente ambas magnitudes es precisamente el valor R en ohmios (Ω) de la resistencia.
4–3
)()( tRitv =
La impedancia operacional, según su definición, será RsZ =)( .
• Bobina: componente pasivo que almacena energía magnética en función de la corriente que circula por ella. En este caso, la diferencia de tensión v(t) entre los terminales de la bobina es directamente proporcional a la derivada temporal de la corriente i(t) que circula por ella. La constante de proporcionalidad ente ambas magnitudes es el coeficiente de autoinducción L, medido en henrios (H) en el Sistema Internacional.
dttdiLtv )()( =
La impedancia operacional , según su definición, será LssZ =)( .
• Condensador: componente pasivo que almacena energía eléctrica en función de la diferencia de tensión en sus terminales. En este caso, la corriente i(t) que circula por el condensador es directamente proporcional a la derivada temporal de la diferencia de tensión v(t) en sus terminales. La constante de proporcionalidad ente ambas magnitudes es la capacidad C, medido en faradios (F) en el sistema internacional.
i(t) =C dv(t)dt
La impedancia operacional , según su definición, es Cs
sZ 1)( = .
v
i
+ _
+ - v
i
+
_
v
i
+ _
4–4
Ejemplo 4.1. Considérese el circuito de la figura 4.1. Se trata de un circuito con tres mallas, una fuente independiente de tensión vi(t), una bobina de autoinducción L, un condensador de capacidad C y tres resistencias de valores R1, R2 y R3. El objetivo es obtener una función de transferencia entre la tensión de la fuente vi(t) (entrada del sistema) y la corriente io(t) que circula por la resistencia R3 (salida del sistema). La elección de la salida es completamente arbitraria y podría ser cualquier otra variable de interés en el circuito.
Figura 4.1. Circuito eléctrico
Para conseguir el objetivo propuesto, se aplicarán tres procedimientos diferentes con el fin de ilustrar las diversas formas de cálculo de la función de transferencia a partir de la teoría de circuitos.
El primer procedimiento consta de los siguientes pasos:
• Identificación de las mallas del circuito y definición de las corrientes de malla: En este caso el circuito consta de tres mallas con corrientes i1, i2 e i3, respectivamente.
• Se aplica la primera ley de Kirchoff a cada malla usando impedancias operacionales y transformadas de Laplace de todas las variables eléctricas.
( )31111 IICs
IRVi −+=
( )32220 IIRLsI −+=
0 = 1Cs
I3 − I1( )+ R2 I3 − I2( )+ R3I3
• A continuación, estas ecuaciones de malla se ordenan en forma de ecuación matricial.
R1
C
io
R2
R3
+ -
- +
vi vC
iL
iC
+ -
vL
i1 i2
i3
+ -
- +
+ -
4–5
⎥⎥⎥
⎦
⎤
⎢⎢⎢
⎣
⎡
⎥⎥⎥⎥⎥
⎦
⎤
⎢⎢⎢⎢⎢
⎣
⎡
++−−
−+
−+
=⎥⎥⎥
⎦
⎤
⎢⎢⎢
⎣
⎡
3
2
1
)(
322
22
1
110
101
00
III
CsRRR
Cs
RLsRCsCs
RV
sZ
i
Nótese que la matriz Z(s), denominada matriz de impedancias operacionales, es una matriz simétrica siempre que no haya fuentes dependientes en el circuito y los sentidos de las corrientes de malla coincidan. En este caso, la diagonal principal contiene en la posición i la suma de las impedancias operacionales presentes en la malla i. Por otra parte, el elemento de la fila i y la columna j, coincide con la suma, cambiada de signo, de las impedancias operacionales compartidas por las mallas i y j. Teniendo en cuenta que esta estructura se mantiene, no sería necesario, en los supuestos mencionados, pasar por las ecuaciones de malla, pudiéndose construir directamente la ecuación matricial a partir de la topología del circuito.
• El siguiente paso consiste en calcular las funciones de transferencia entre la tensión de la fuente y las corrientes de malla. Para ello, hay que resolver el sistema de ecuaciones matricial anterior, o bien calculando la inversa de la matriz de impedancias operacionales, o bien utilizando algún método de resolución de sistemas de ecuaciones, por ejemplo la regla de Cramer. Aplicando dicha regla, resulta:
( )
( ) ( ) ( )
( )
( ) ( ) ( )312
3213212
321
232
232
312
321321321
23232322
22
1
1)(
10
0
101
RRCRsRRRRRR
CLsRRLR
CRsRR
CLLsRR
sRR
CRRRRRRR
CLsRRLR
CsRRR
CLLsRR
sZCs
RRR
RLsRCs
VIi
++⎟⎠⎞⎜
⎝⎛ +++++
+⎟⎠⎞⎜
⎝⎛ +++
=
=+++++++
++++=
++−
−+
−
=
4–6
( ) ( ) ( )
( ) ( ) ( )312
3213212
321
2
312
321321321
232
2
1
2
1)(
10100
111
RRCRsRRRRRR
CLsRRLR
CR
sRR
CRRRRRRR
CLsRRLR
CsR
sZCs
RRCs
RCsCs
R
VIi
++⎟⎠⎞⎜
⎝⎛ +++++
=
=+++++++
=++−
−
−+
=
( ) ( ) ( )
( ) ( ) ( )312
3213212
321
2
312
321321321
22
2
1
3
1)(
0100
101
RRCRsRRRRRR
CLsRRLR
CRs
CL
sRR
CRRRRRRR
CLsRRLR
CsR
CL
sZ
RCs
LsRCs
R
VIi
++⎟⎠⎞⎜
⎝⎛ +++++
+=
=+++++++
+=
−−
+
+
=
• Por último, se relaciona la variable de salida con las corrientes de malla para obtener la función de transferencia final. Nótese que en el paso anterior sólo es necesario obtener las corrientes de malla que intervengan en el cálculo de la variable de salida. Además en este caso, la relación de la salida con las corrientes de malla es trivial, ya que la corriente io coincide con la corriente i3.
( ) ( )( ) ( )3123213212
321
23
RRRsCRRRRRRLsRRLCRRLs
VI
VI
ii
o
++++++++==
La función de transferencia también se puede calcular usando el teorema de Thevenin. Este segundo procedimiento consta de los siguientes pasos:
• En primer lugar se calcula la tensión de Thevenin Vth y la impedancia de Thèvenin Zth del dipolo de tensión equivalente en los terminales de la resistencia R3.
11
1
1
11
+=
+=
CsRV
RCs
CsVV iith
4–7
11
1
1
1
2
2
1
1
2
2
++
+=
++
+=
CsRR
RLsLsR
RCs
RCs
RLsLsRZth
• Finalmente, se conecta la resistencia R3 al dipolo de Thevenin y se calcula la corriente io por la resistencia R3 de forma simple, ya que todas las impedancias del circuito equivalente están en serie.
Io =Vth
Zth + R3=
Vi1
R1Cs+1R2LsLs+ R2
+R1
R1Cs+1+ R3
Operando, la función de transferencia coincide con la obtenida aplicando el primer procedimiento.
( ) ( ) ( )( )
( ) ( )( ) ( )3123213212
321
2
2132112
2
31
1
2
2
1
111
11
RRRsCRRRRRRLsRRLCRRLs
RLsCsRRRLsRCsRLsRRLs
RCsRR
RLsLsR
CsRVI
i
o
++++++++=
=++++++
+=+
++
+
+=
El tercer y último procedimiento consiste en construir un diagrama de bloques para el circuito y utilizar el álgebra de diagrama de bloques para obtener la función de transferencia que se desee. Con el fin de que este diagrama de bloques sea útil para simular la respuesta del circuito, tanto libre como forzada, y que tengamos acceso no sólo a la variable de salida, sino también a todas las variables intermedias que pudieran ser de interés, se impondrá una restricción a la hora de construirlo: sólo deben aparecer en el diagrama ganancias, puntos de suma e integradores (bloques del tipo 1/s). Este procedimiento consta de los siguientes pasos:
• Se usa un integrador por cada elemento que almacene energía en el circuito: bobinas y condensadores. En el caso de las bobinas, la entrada al integrador será la derivada temporal de la corriente y la salida será la corriente. En el caso de los condensadores, la entrada al integrador será la derivada temporal de la tensión y la salida la tensión.
• Se obtienen, a partir del circuito, las ecuaciones que permiten calcular la variable de entrada de cada integrador (derivadas temporales de corriente en las bobinas o de tensión en los condensadores) en función de las variables de salida de todos los integradores (tensiones de los condensadores y corrientes de las bobinas), de la variables de entrada del resto de integradores y de las variables de entrada del circuito (fuentes de tensión o de corriente independientes). Para obtener la ecuación correspondiente a la
4–8
derivada temporal de la corriente de una bobina (proporcional a la tensión de la bobina) se usa la segunda ley de Kirchoff aplicada a una malla que contenga la bobina. Para obtener la ecuación correspondiente a la derivada temporal de la tensión de un condensador (proporcional a la corriente del condensador) se usa la primera ley de Kirchoff aplicada a un nudo al que esté conectado el condensador. Es imprescindible que todos los parámetros que afecten al comportamiento del circuito aparezcan en estas ecuaciones.
• Mediante un sumador, colocado a la entrada de cada integrador, se construyen gráficamente las ecuaciones deducidas previamente completando el diagrama de bloques.
• Se identifica la salida el diagrama de bloques, o bien, si no está presente, se obtiene una ecuación adicional que relaciona la variable de salida con el resto de variables que sí aparecen en el diagrama de bloques: entradas y tensiones y corrientes de bobinas y condensadores. Mediante un sumador adicional se construye la ecuación de salida en el diagrama.
• Finalmente, se reduce el diagrama de bloques empleando el álgebra de diagrama de bloques para obtener la función de transferencia deseada.
Para el circuito de la figura 4.1, las ecuaciones que permiten dibujar el diagrama de bloques son las siguientes:
1 2
C i C LC L
dv v v vi C idt R R
+= = − + +
32
L LL C L
di vv L v R idt R
⎛ ⎞= = − − +⎜ ⎟
⎝ ⎠
2
Lo L
vi iR
= +
El diagrama de bloques resultante en Simulink se muestra en la figura 4.2:
iC dvC/dt vC
io
vL1io
1s
1s
R3
1/L1/C
1/R2
1/R11vi
Figura 4.2. Diagrama de bloques del circuito eléctrico
4–9
Se propone como ejercicio de aplicación del álgebra de diagrama de bloques la demostración de que la función de transferencia resultante al reducir este diagrama de bloques es la calculada mediante los dos procedimientos previos.
4.2 Circuitos electrónicos con amplificadores operacionales
Como un caso particular de circuitos eléctricos con fuentes de tensión dependientes de tensión, se ilustra en esta sección cómo obtener funciones de transferencia en circuitos electrónicos con amplificadores operacionales. El estudio detallado de un amplificador operacional no es objeto de estudio en este capítulo y se supone que el lector ha adquirido esos conocimientos en un curso básico de Electrónica. Sólo se expondrá, a modo de recordatorio, las propiedades fundamentales de un amplificador operacional ideal y el procedimiento a aplicar para obtener funciones de transferencia en circuitos que contengan este tipo de amplificadores.
Un amplificador operacional ideal es un dispositivo activo que requiere alimentación externa con dos terminales de entrada y un terminal de salida. Para representar gráficamente este componente en un circuito, se emplea un símbolo en forma de triángulo, tal como se observa en la figura 4.3. Los dos terminales de entrada, denominados inversor y no inversor, se indican mediante signos – y +, respectivamente.
El amplificador operacional se comporta como un amplificador diferencial con una resistencia de entrada y una ganancia muy elevadas y una resistencia de salida muy baja. Para analizar circuitos electrónicos con amplificadores operacionales, se suele usar el denominado amplificador operacional ideal que se caracteriza por tener resistencia de entrada infinita, resistencia de salida nula y ganancia infinita. La ganancia infinita implica que se requiere una tensión diferencial nula para obtener una tensión finita en la salida.
A la hora de analizar circuitos que contengan este componente, se pueden aplicar dos reglas sencillas que permiten calcular cualquier función de transferencia que se requiera:
1. El amplificador operacional ideal no consume corriente por sus terminales de entrada debido a su resistencia de entrada infinita.
2. El amplificador operacional ideal realimentado negativamente intenta igualar los valores de tensión en sus dos terminales de entrada.
En la segunda regla, se hace énfasis en el matiz de que lo intenta porque sólo lo conseguirá si la tensión que fijan en la salida el resto de componentes del circuito está dentro de los límites de saturación del amplificador, impuestos por las tensiones de alimentación. De todas formas, se supondrá que el amplificador operacional trabaja siempre en la zona lineal, descartando la posibilidad de que pueda saturar en ciertas circunstancias.
4–10
Existen dos esquemas habituales a la hora de emplear un amplificador operacional: la configuración inversora y la no inversora. Aunque estos son los esquemas que aparecen con mayor frecuencia en circuitos electrónicos lineales, podemos encontrarnos con otros circuitos que no se corresponden con estas configuraciones típicas, pero que pueden analizarse aplicando las reglas mencionadas previamente. A continuación se deducen las funciones de transferencia entre tensión de entrada y tensión de salida para estas dos configuraciones típicas.
4.1.1 Amplificador inversor
El esquema de un circuito con amplificador operacional en configuración inversora se muestra en la figura 4.3. Las impedancias Z1 y Z2 representan las impedancias equivalentes de cualquier circuito pasivo compuesto de resistencias, condensadores y bobinas conectados de cualquier forma.
Figura 4.3. Amplificador operacional en configuración inversora
Para obtener la función de transferencia entre la tensión de entrada vi y la tensión de salida vo, se emplean las dos reglas mencionadas previamente. Aplicando la primera regla, se deduce que la tensión v- del terminal inversor de entrada del amplificador operacional es 0, ya el terminal no inversor de entrada está conectado a masa. Aplicando la segunda regla, se concluye que las corrientes i1 e i2 han de ser iguales ya que el amplificador operacional no consume corriente en sus terminales de entrada. Por lo tanto, resulta:
1 21 2
( ) 0 0 ( )( ) ( )( ) ( )
i oV s V sI s I sZ s Z s
− −= = =
2
1
( ) ( )( )( ) ( )o
i
V s Z sG sV s Z s
= = −
4.1.2 Amplificador no inversor
El esquema de un circuito con amplificador operacional en configuración inversora se muestra en la figura 4.4.
vi + -
vo
Z2
Z1
i2
i1
_
+
+ _
4–11
Figura 4.4. Amplificador operacional en configuración no inversora
Aplicando la primera regla, se deduce que la tensión v- del terminal inversor de entrada del amplificador operacional es igual a vi, ya el terminal no inversor está conectado a la fuente que proporciona la tensión de entrada. Aplicando la segunda regla, se concluye que las corrientes i1 e i2 han de ser iguales ya que el amplificador operacional no consume corriente en sus terminales de entrada. Por lo tanto, resulta:
1 21 2
0 ( ) ( ) ( )( ) ( )( ) ( )i i oV s V s V sI s I s
Z s Z s− −= = =
2
1
( ) ( )( ) 1( ) ( )o
i
V s Z sG sV s Z s
= = +
4.3 Sistemas mecánicos de traslación En esta sección se presenta el modelado de sistemas mecánicos en movimiento de traslación suponiendo comportamiento lineal e invariante en el tiempo. Sólo se requiere un conocimiento de los principios básicos de la mecánica de Newton para obtener una función de transferencia en este tipo de sistemas. La entrada de la función de transferencia será típicamente una fuerza aplicada en algún punto del sistema, mientras que la salida puede ser cualquier variable mecánica de interés, ya sea una posición, una velocidad o una aceleración. Como paso previo al cálculo de funciones de transferencia en sistemas mecánicos de traslación, es necesario introducir el concepto de impedancia operacional Z(s) de un componente mecánico (masa, muelle o fricción viscosa) como el cociente entre la transformada de Laplace F(s) de la fuerza que apliquemos sobre el elemento en cuestión y la transformada de Laplace X(s) de su desplazamiento, en ausencia de condiciones iniciales.
nulasicsXsFsZ
..)()()( ⎟⎟⎠
⎞=
A continuación se presentan las relaciones entre la fuerza aplicada y el desplazamiento, así como la impedancia operacional resultante, para cada
vo
Z2
Z1
i2
i1
_
+
+ _ vi + -
4–12
uno de los componentes que pueden aparecer en un sistema mecánico de traslación.
• Masa: componente que almacena energía cinética debido a su velocidad. Según el principio de acción y reacción, al aplicarle una fuerza de acción f(t) a una masa aparece una fuerza de reacción de tipo inercial proporcional a su aceleración o segunda derivada temporal de su desplazamiento x(t). La constante de proporcionalidad entre ambas magnitudes es precisamente la masa M en kilogramos (Kg).
2
2 )()(dttxdMtf =
La impedancia operacional, según su definición, es 2)( MssZ = .
• Muelle: componente que almacena energía potencial por deformación. Al aplicarle una fuerza de acción f(t) a un muelle, aparece una fuerza de reacción proporcional a su deformación x(t). La constante de proporcionalidad entre ambas magnitudes es la constante K del muelle expresada en N/m en el Sistema Internacional.
)()( tKxtf =
Su impedancia operacional resulta KsZ =)( .
• Fricción viscosa: componente que representa la presencia en el sistema mecánico de una fuerza de rozamiento de tipo viscoso, es decir, proporcional a la velocidad. El símbolo que se utiliza para representar gráficamente este efecto se corresponde con la sección transversal de un cilindro repleto de un fluido (aire o aceite) en cuyo interior se mueve un émbolo encontrando una fuerza oponente a su desplazamiento precisamente de tipo viscoso. Conviene aclarar que el hecho de utilizar este símbolo no significa que todos los rozamientos de tipo viscoso que podamos encontrar en sistemas mecánicos se correspondan siempre con este dispositivo físico. Cuando a un elemento de fricción viscosa se le aplica una fuerza de
f(t)
x(t)
M
K
f(t) x(t)
4–13
acción f(t), éste opone una fuerza de reacción proporcional a la velocidad relativa entre los elementos que friccionan (émbolo y cilindro, a través del fluido, en el ejemplo físico) o derivada temporal del desplazamiento relativo x(t) entre ambos elementos. La constante de proporcionalidad entre ambas magnitudes es la constante D expresada en N.s/m en el Sistema Internacional.
dttdxDtf )()( =
En este caso, la impedancia operacional vale DssZ =)( .
Ejemplo 4.2. Considérese el sistema mecánico de traslación de la figura 4.5. Se trata de un sistema mecánico con dos grados de libertad o movimientos independientes con desplazamientos asociados x1 y x2 cuyo sentido positivo se muestra en la figura. Sobre la masa M1 se aplica una fuerza f y se desea obtener la función de transferencia entre dicha fuerza (variable de entrada) y la velocidad relativa entre las dos masas (variable de salida). Como ya se comentó en el caso de los circuitos eléctricos, la elección de la salida es completamente arbitraria y podría ser cualquier otra variable de interés en el sistema mecánico.
Figura 4.5. Sistema mecánico de traslación
En primer lugar se obtendrán las ecuaciones de equilibrio de fuerzas en cada uno de los dos grados de libertad del sistema. En la ecuación de cada grado de libertad se igualan las fuerzas de acción y reacción aplicando la tercera ley de Newton. A la hora de sumar fuerzas de reacción sobre cada grado de libertad se aplica el principio de superposición: se suman por separado las fuerzas de reacción sobre el grado de libertad en cuestión provocadas por desplazamientos en sentido positivo del mismo grado de libertad y de cada
K1
K2
M1
M2
D2 f
D1 x1
x2
D
x(t)
f(t)
4–14
uno de los grados de libertad restantes. A esta técnica se la denomina diagrama del cuerpo libre. Para el sistema mecánico de la figura 4.5, resultan las siguientes ecuaciones para los dos grados de libertad existentes:
21 1 1 2
1 1 1 1 2 2 1 2 2 22
d x dx dx dxf M D K x D K x D K xdt dt dt dt
= + + + + − −
22 2 1
2 2 2 2 2 2 120 d x dx dxM D K x D K xdt dt dt
= + + − −
Para obtener la función de transferencia deseada, se aplicarán dos procedimientos diferentes
El primer procedimiento consta de los siguientes pasos:
• Se aplica la transformada de Laplace a las ecuaciones de equilibrio de fuerzas de cada grado de libertad:
21 1 1 1 1 1 2 1 2 1 2 2 2 2( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )F s M s X s D sX s K X s D sX s K X s D sX s K X s= + + + + − −
22 2 2 2 2 2 2 1 2 10 ( ) ( ) ( ) ( ) ( )M s X s D sX s K X s D sX s K X s= + + − −
• Estas ecuaciones se ordenan en forma de ecuación matricial.
F0
!
"#
$
%&=
M1s2 + (D1 +D2 )s+K1 +K2 −D2s−K2
−D2s−K2 M2s2 +D2s+K2
!
"
##
$
%
&&
Z (s)
X1X2
!
"##
$
%&&
Nótese que la matriz de impedancias operacionales Z(s) es una matriz simétrica siempre que coincidan los sentidos positivos de los desplazamientos de los grados de libertad del sistema. En este caso, la diagonal principal contiene en la posición i la suma de las impedancias operacionales de todos los elementos conectados al grado de libertad i. Por otra parte, el elemento de la fila i y la columna j coincide con la suma, cambiada de signo, de las impedancias operacionales de los elementos compartidos por los grados de libertad i y j. Teniendo en cuenta que esta estructura se mantiene, no sería necesario, en el supuesto mencionado, pasar por las ecuaciones de equilibrio de fuerzas en cada grado de libertad, pudiéndose construir directamente la ecuación matricial a partir de la topología del sistema.
• El siguiente paso consiste en calcular las funciones de transferencia entre la fuerza f y los desplazamientos xi de cada grado de libertad. Para ello, hay que resolver el sistema de ecuaciones matricial anterior, o bien calculando la inversa de la matriz de impedancias
4–15
operacionales, o bien utilizando algún método de resolución de sistemas de ecuaciones, como por ejemplo la regla de Cramer. Aplicando dicha regla, resulta:
( ) ( )
2 22
2 2 21
22 2 2
4 3 21 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2
10
( )
D s KM s D s KX
F Z s
M s D s KM M s M D M D M D s M K M K M K DD s K D s K K
− −⎡ ⎤⎢ ⎥+ +⎣ ⎦= =
+ +=+ + + + + + + + +
( ) ( )
21 1 2 1 2
2 22
2 24 3 2
1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2
( ) 10
( )
M s D D s K KD s KX
F Z sD s K
M M s M D M D M D s M K M K M K DD s K D s K K
⎡ ⎤+ + + +⎢ ⎥− −⎣ ⎦= =
+=+ + + + + + + + +
• Por último, se relaciona la variable de salida, en este caso la velocidad relativa entre las dos masas, con los desplazamientos de los grados de libertad para obtener la función de transferencia final. Nótese que en el paso anterior sólo es necesario calcular los desplazamientos de los grados de libertad que intervengan en el cálculo de la variable de salida.
( ) ( )( ) ( )
( ) ( )
1 2
22 2 2 2 2
4 3 21 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2
32
4 3 21 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2
sX sXYF F
s M s D s K s D s KM M s M D M D M D s M K M K M K D D s K D s K K
M sM M s M D M D M D s M K M K M K D D s K D s K K
−= =
+ + − += =
+ + + + + + + + +
=+ + + + + + + + +
Otro procedimiento alternativo consiste en construir un diagrama de bloques para el sistema mecánico y utilizar el álgebra de diagrama de bloques para obtener la función de transferencia que se desee. Con el fin de que este diagrama de bloques sea útil para simular la respuesta del sistema mecánico, tanto libre como forzada, y que estén accesibles no sólo la variable de salida, sino todas las variables intermedias, únicamente deben aparecer en el diagrama ganancias, puntos de suma e integradores (bloques del tipo 1/s). Este procedimiento consta de los siguientes pasos:
• Se disponen dos integradores en serie para cada grado de libertad que permitan calcular, a partir de la aceleración (entrada del primer integrador), la velocidad (salida del primer integrador) y, a partir de ésta (entrada del segundo integrador), la posición (salida del segundo integrador) del grado de libertad correspondiente. Si alguno de los grados de libertad no tiene asociada una masa, se prescinde
4–16
del primer integrador ya que no aparece la aceleración en la ecuación de equilibrio de fuerzas de ese grado de libertad.
• Se despeja la aceleración, o en su defecto la velocidad, de la ecuación de equilibrio de fuerzas para cada grado de libertad. Obsérvese que el resto de variables que aparecen en estas ecuaciones ya están presentes en el diagrama de bloques o son entradas del sistema.
• Mediante un sumador, colocado a la entrada de cada integrador, se construyen gráficamente las ecuaciones algebraicas deducidas previamente completando el diagrama de bloques.
• Se identifica la salida en el diagrama de bloques, o bien, si no está presente, se obtiene una ecuación adicional que relaciona la variable de salida con el resto de variables que sí aparecen en el diagrama de bloques: entradas y aceleraciones, velocidades y posiciones de cada grado de libertad. Mediante un sumador adicional se construye la ecuación de salida en el diagrama de bloques, si fuese necesario.
• Finalmente, se reduce el diagrama de bloques empleando el álgebra de diagrama de bloques para obtener la función de transferencia deseada.
Para el sistema mecánico de traslación de la figura 4.5, la ecuaciones que permiten dibujar el diagrama de bloques son las siguientes:
21 1 1 2
1 1 1 2 2 1 2 2 221
1d x dx dx dxf D K x D K x D K xdt M dt dt dt
⎛ ⎞= − − − − + +⎜ ⎟⎝ ⎠
22 2 1
2 2 2 2 2 122
1d x dx dxD K x D K xdt M dt dt
⎛ ⎞= − − + +⎜ ⎟⎝ ⎠
Finalmente, la ecuación de salida correspondiente a la velocidad relativa entre las dos masas resulta:
1 2dx dxydt dt
= −
El diagrama de bloques final en Simulink se muestra en la figura 4.6:
4–17
d2X1/dt2 dx1/dt
x1 d2X2/dt2
dx2/dt
x2
1y
1s
1s
1s
1s
D2
K2
K1+K2
K2
D1+D2
1/M2
D2D2
1/M11f
Figura 4.6. Diagrama de bloques del sistema mecánico de traslación
Se propone, como ejercicio de aplicación del álgebra de diagrama de bloques, la demostración de que la función de transferencia resultante al reducir este diagrama de bloques es la calculada mediante el primer procedimiento.
Téngase en cuenta, que la utilidad fundamental del diagrama de bloques es su uso en un entorno gráfico como Simulink, donde es posible, a partir de este diagrama de bloques, simular tanto la respuesta forzada como la respuesta libre y acceder a cualquier variable intermedia sin dificultad. Como procedimiento de cálculo manual de la función de transferencia no facilita los cálculos, si se compara con el primer procedimiento, salvo que estos cálculos se acometan de forma automática mediante Simulink y usando valores numéricos para todos los parámetros.
4.4 Sistemas mecánicos de rotación A continuación se presenta el modelado de sistemas mecánicos con movimiento de rotación suponiendo comportamiento lineal e invariante en el tiempo. Para modelar este tipo de sistemas sólo se requiere un conocimiento de los principios básicos de la mecánica de Newton aplicada al movimiento de rotación. La entrada de la función de transferencia será típicamente el par aplicado en algún punto del sistema, mientras que la salida puede ser cualquier variable mecánica de interés, ya sea una posición, una velocidad o una aceleración angulares. Como se comprobará, el planteamiento es muy similar al que se acaba de exponer para sistemas mecánicos de traslación. Como paso previo al cálculo de funciones de transferencia en sistemas mecánicos de rotación, es necesario introducir el concepto de impedancia operacional Z(s) de un componente mecánico (elemento inercial, muelle o fricción viscosa) como el cociente entre la transformada de Laplace T(s) del par que apliquemos sobre el elemento en cuestión y la transformada de Laplace θ(s) de su desplazamiento angular en ausencia de condiciones iniciales.
. .
( )( )( ) c i nulas
T sZ ssθ⎞
= ⎟⎠
4–18
A continuación se presentan las relaciones entre el par aplicado y el desplazamiento angular, así como la impedancia operacional resultante, para cada uno de los componentes que pueden aparecer en un sistema mecánico de rotación. El sentido de las flechas (horario o anti-horario) marca el sentido que se considera como positivo cuando se observa el sistema mecánico de rotación desde la izquierda.
• Elemento inercial: componente que almacena energía cinética debido a su velocidad de giro. Según la tercera ley de Newton o principio de acción y reacción, al aplicarle un par de acción T(t) a una masa aparece un par de reacción de tipo inercial proporcional a su aceleración angular o segunda derivada temporal de su desplazamiento angular θ(t). La constante de proporcionalidad entre ambas magnitudes es el momento de inercia J, en Kg.m2 o N.m.s2, de la masa giratoria con respecto al eje de rotación.
2
2
( )( ) d tT t Jdtθ=
La impedancia operacional , según su definición, es 2( )Z s Js= .
• Muelle: componente mecánico que almacena energía potencial por deformación angular. Al aplicarle una par de acción T(t) a un muelle aparece un par de reacción proporcional a su deformación angular θ(t). La constante de proporcionalidad entre ambas magnitudes es la constante K de torsión del muelle expresada en N.m en el Sistema Internacional.
( ) ( )T t K tθ=
Su impedancia operacional resulta KsZ =)( .
• Fricción viscosa: componente que representa la presencia en el sistema mecánico de un par de rozamiento de tipo viscoso, es decir proporcional a la velocidad angular. El símbolo que se utiliza para
T θ
K
θ
J
T
4–19
representar gráficamente este efecto se corresponde con la sección transversal de un cilindro repleto de un fluido (aire o aceite) en cuyo interior gira un émbolo que encuentra un par oponente a su desplazamiento angular precisamente de tipo viscoso. Conviene aclarar que el hecho de utilizar este símbolo no significa que todos los pares de rozamientos de tipo viscoso en sistemas mecánicos de rotación se correspondan siempre con este dispositivo físico. Cuando a un elemento de fricción viscosa se le aplica un par de acción T(t), éste opone un par de reacción proporcional a la velocidad angular relativa entre los elementos que friccionan (émbolo y cilindro a través del fluido en el ejemplo físico) o derivada temporal del desplazamiento angular relativo θ(t) entre ambos elementos. La constante de proporcionalidad entre ambas magnitudes es la constante de fricción viscosa D expresada en N.m.s en el Sistema Internacional.
T (t) = D dθ(t)dt
En este caso, la impedancia operacional vale DssZ =)( .
Ejemplo 4.3. Considérese el sistema mecánico de rotación de la figura 4.7. Se trata de un sistema mecánico con dos grados de libertad o movimientos independientes con desplazamientos angulares asociados θ1 y θ2 con sentido positivo el mostrado en la figura. Sobre la masa de momento de inercia J se aplica un par T y se desea obtener la función de transferencia entre dicho par (variable de entrada) y la velocidad angular de deformación del muelle con constante K2 (variable de salida). Como ya se comentó en casos anteriores, la elección de la salida es completamente arbitraria y podría ser cualquier otra variable de interés en el sistema mecánico.
Figura 4.7. Sistema mecánico de rotación
T θ1
D1
D2
J
K1
K2
θ2
T θ
D
4–20
En primer lugar, se obtendrán las ecuaciones de equilibrio de pares en cada uno de los dos grados de libertad del sistema. En la ecuación de cada grado de libertad se igualan los pares de acción y reacción aplicando la tercera ley de Newton. A la hora de sumar pares de reacción sobre cada grado de libertad se aplica el principio de superposición, sumando por separado los pares de reacción sobre el grado de libertad en cuestión provocado por desplazamientos angulares en sentido positivo del mismo grado de libertad y de cada uno de los grados de libertad restantes. Para el sistema mecánico de la figura 4.7, resultan las siguientes ecuaciones para los dos grados de libertad existentes:
T = J d2θ1dt2
+D1dθ1dt
+K1θ1 +D2dθ1dt
−D2dθ2dt
2 12 2 2 20 d dD K Ddt dtθ θθ= + −
Para obtener la función de transferencia deseada se aplicarán dos procedimientos diferentes.
El primer procedimiento consta de los siguientes pasos:
• Se aplica la transformada de Laplace a las ecuaciones de equilibrio de pares de cada grado de libertad:
T (s) = Js2θ1(s)+D1sθ1(s)+K1θ1(s)+D2sθ1(s)−D2sθ2 (s)
0 = D2sθ2 (s)+K2θ2 (s)−D2sθ1(s)
• Estas ecuaciones se ordenan en forma de ecuación matricial.
T0
!
"#
$
%&=
Js2 + (D1 +D2 )s+K1 −D2s−D2s D2s+K2
!
"
##
$
%
&&
Z (s) θ1θ2
!
"##
$
%&&
Nótese que la matriz de impedancias operacionales Z(s) es una matriz simétrica siempre que coincidan los sentidos positivos de los desplazamientos angulares de los grados de libertad del sistema. En este caso, la diagonal principal contiene en la posición i la suma de las impedancias operacionales de todos los elementos conectados al grado de libertad i. Por otra parte, el elemento de la fila i y la columna j coincide con la suma, cambiada de signo, de las impedancias operacionales de los elementos compartidos por los grados de libertad i y j. Teniendo en cuenta que esta estructura se mantiene, no sería necesario plantear previamente las ecuaciones de equilibrio de pares en cada grado de libertad, pudiéndose construir directamente la ecuación matricial a partir de la topología del sistema.
4–21
• El siguiente paso consiste en calcular las funciones de transferencia entre el par T y los desplazamientos θi de cada grado de libertad. Para ello, hay que resolver el sistema de ecuaciones matricial anterior, o bien calculando la inversa de la matriz de impedancias operacionales, o bien utilizando algún método de resolución de sistemas de ecuaciones, por ejemplo la regla de Cramer. Aplicando dicha regla, resulta:
( ) ( )
2
2 21
2 23 2
2 2 1 2 1 2 2 2 2 1 1 2
10
( )
D sD s K
T Z sD s K
JD s JK D D s D K D K D K s K K
θ−⎡ ⎤
⎢ ⎥+⎣ ⎦= =
+=+ + + + + +
( ) ( )
21 2 1
22
23 2
2 2 1 2 1 2 2 2 2 1 1 2
( ) 10
( )
Js D D s KD s
T Z sD s
JD s JK D D s D K D K D K s K K
θ⎡ ⎤+ + +⎢ ⎥−⎣ ⎦= =
=+ + + + + +
• Por último, se relaciona la variable de salida, en este caso la velocidad angular de deformación del muelle de constante K2, con los desplazamientos de los grados de libertad para obtener la función de transferencia final. Nótese que en el paso anterior sólo es necesario calcular los desplazamientos de los grados de libertad que intervengan en el cálculo de la variable de salida. Por lo tanto, sólo sería necesario calcular la segunda función de transferencia.
YT=sθ2T
=D2s
2
JD2s3 + JK2 +D1D2( )s2 + D1K2 +D2K2 +D2K1( )s+K1K2
Otro procedimiento alternativo consiste en construir un diagrama de bloques para el sistema mecánico de rotación y utilizar el álgebra de diagrama de bloques para obtener la función de transferencia que se desee. Con el fin de que este diagrama de bloques sea útil para simular la respuesta del sistema, tanto libre como forzada, y que sean accesibles no sólo a la variable de salida, sino también todas las variables intermedias, únicamente deben aparecer en el diagrama de bloques ganancias, puntos de suma e integradores (bloques del tipo 1/s). Este procedimiento consta de los siguientes pasos:
• Se disponen dos integradores en serie para cada grado de libertad que permiten calcular, a partir de la aceleración angular (entrada del primer integrador), la velocidad angular (salida del primer integrador), y a partir de ésta (entrada del segundo integrador), la posición angular (salida del segundo integrador) del grado de libertad correspondiente. Si alguno de los grados de libertad no tiene asociada una masa, situación que se da en el ejemplo de la figura 4.7, se prescinde del primer integrador ya que no aparece la aceleración angular en la ecuación de equilibrio de pares de ese grado de libertad.
4–22
• Se despeja la aceleración angular, o en su defecto la velocidad angular, de la ecuación de equilibrio de pares para cada grado de libertad. Obsérvese que el resto de variables que aparecen en estas ecuaciones ya están presentes en el diagrama de bloques o son entradas del sistema.
• Mediante un sumador, colocado a la entrada de cada integrador, se construyen gráficamente las ecuaciones deducidas previamente completando el diagrama de bloques.
• Se identifica la salida en el diagrama de bloques, o bien, si no está presente, se obtiene una ecuación adicional que relacione la variable de salida con el resto de variables que sí aparecen en el diagrama de bloques: entradas y aceleraciones, velocidades y posiciones angulares de cada grado de libertad. Mediante un sumador adicional, se construye la ecuación de salida en el diagrama de bloques si fuese necesario.
• Finalmente, se reduce el diagrama de bloques empleando el álgebra de diagrama de bloques para obtener la función de transferencia deseada.
Para el sistema mecánico de rotación de la figura 4.7, la ecuaciones que permiten dibujar el diagrama de bloques son las siguientes:
21 1 1 2
1 1 1 2 22
1d d d dT D K D Ddt J dt dt dtθ θ θ θθ⎛ ⎞= − − − +⎜ ⎟⎝ ⎠
2 12 2 2
2
1d dK Ddt D dtθ θθ⎛ ⎞= − +⎜ ⎟⎝ ⎠
Finalmente, la ecuación de salida, correspondiente a velocidad angular de deformación del muelle de constante K2, resulta:
2dydtθ=
El diagrama de bloques final en Simulink se muestra en la figura 4.8:
Figura 4.8. Diagrama de bloques del sistema mecánico de rotación
4–23
Se propone como ejercicio de aplicación del álgebra de diagrama de bloques la demostración de que la función de transferencia resultante al reducir este diagrama de bloques es la calculada mediante el primer procedimiento.
4.5 Sistemas térmicos
En esta sección se presenta el modelado de sistemas térmicos suponiendo comportamiento lineal e invariante en el tiempo. Se denomina sistema térmico a un sistema compuesto de varios medios en contacto, con temperaturas que cambian por el almacenamiento e intercambio de energía térmica. Además se considera un medio exterior en el sistema térmico que posee la peculiaridad de poder almacenar o intercambiar energía térmica con el resto de medios sin que afecte a su temperatura. La temperatura del medio exterior puede cambiar, pero nunca por su interacción con el resto de medios del sistema. Se supone un valor uniforme de la temperatura en cada medio, ya que en caso contrario se requieren ecuaciones en derivadas parciales para modelar la transmisión de energía térmica en el interior de cada medio y entre medios.
Para modelar este tipo de sistemas, sólo se necesitan manejar las leyes que rigen el almacenamiento de energía térmica en un medio y la transferencia de energía térmica entre dos medios con diferente temperatura. A la hora de obtener el modelo o función de transferencia del sistema térmico, la entrada será o bien la potencia térmica generada internamente en alguno de los medios o bien la temperatura del medio exterior, mientras que la salida será la temperatura de cualquiera de los medios o alguna variable relacionada directamente con estas temperaturas. A continuación se presentan las ecuaciones que gobiernan el almacenamiento de energía térmica en un medio y la transferencia de energía térmica entre medios a distinta temperatura.
• Almacenamiento de energía térmica en un medio: la potencia Pa con la que se almacena energía térmica Ea en un medio es directamente proporcional a la derivada temporal de su temperatura T, siendo la constante de proporcionalidad la denominada capacidad térmica del medio C, expresada en W.s/ºC en el Sistema Internacional. La capacidad térmica depende de las dimensiones del medio y del material del que esté compuesto.
aadE dTP Cdt dt
= =
• Transmisión de energía térmica entre medios: la potencia Pt transmitida entre dos medios con temperaturas T1 y T2, respectivamente, es directamente proporcional a la diferencia de sus temperaturas, siendo la constante de proporcionalidad el inverso de la denominada resistencia térmica R, expresada en ºC/W en el Sistema Internacional. La resistencia térmica depende de la topología de los medios y de su superficie de contacto así como del material del que estén compuestos ambos medios. Sólo se considera la transmisión de calor por conducción (medios en estado sólido) y convección (uno o ambos medios en estado líquido o gaseoso). Se
4–24
ignora la transferencia de energía térmica por radiación por no ser lineal la ecuación que la gobierna y tener poca relevancia si las temperaturas no son muy elevadas.
1 2tT TPR−=
Ejemplo 4.4. Considérese el sistema térmico de la figura 4.8. Se trata de un sistema que consta de dos medios (medios 1 y 2), uno de ellos en el interior del otro, más el medio exterior (medio 0). Este esquema podría representar varios sistemas térmicos reales como por ejemplo un horno donde el medio interior es el aire dentro del horno y el medio que lo rodea es la pared del horno. También podría representar un modelo térmico de un circuito electrónico integrado en silicio, de tal manera que el medio interior sea el silicio que contiene los componentes del circuito y el medio que lo rodea representa el encapsulado de plástico. Finalmente, también podría representar el modelo térmico simplificado de una vivienda donde el medio interior es el aire dentro de la vivienda y el medio que lo rodea se correspondería con las paredes que limitan la vivienda del medio exterior. Se supone que se genera una potencia térmica Pi en el interior del medio 1 que, en los ejemplos mencionados, podría corresponderse con la potencia disipada por un reostato en el interior del horno, las pérdidas por efecto Joule de los componentes del circuito electrónico o por la potencia suministrada por una bomba de calor instalada en la vivienda para su climatización. En todos los casos el objetivo será obtener dos funciones de transferencia: la que existe entre la potencia térmica generada Pi (entrada) y la temperatura del medio interior T1 (salida) y la que existe entre la temperatura exterior T0 (entrada) y la temperatura del medio interior T1 (salida). Para obtener dichas funciones de transferencia se aplicará el principio de superposición, calculando cada función de transferencia suponiendo que la otra entrada tiene un valor nulo.
Se considera que los medios 1 y 2 tienen capacidades térmicas con valores C1 y C2 y que las resistencias térmicas entre los medios 1 y 2 y entre el medio 2 y el medio exterior son, respectivamente, R12 y R20.
Figura 4.9. Disposición de medios en el sistema térmico del ejemplo 4.4
Para obtener las funciones de transferencia mencionadas anteriormente se requiere, en primer lugar, plantear la ecuación de balance de potencias térmicas para los medios 1 y 2:
2 1 0
4–25
1 1 21 12 1
12i a t
dT T TP P P Cdt R
−= + = +
2 02 2 12 21 20 2
12 20
0 a t tT TdT T TP P P C
dt R R−−= + + = + +
Siendo Pai la potencia con la que se almacena energía térmica en el medio i y Ptij la potencia térmica transferida del medio i al medio j.
A continuación, se aplica la Transformada de Laplace a ambas ecuaciones y se organizan en forma de ecuación matricial:
Pi0
!
"##
$
%&&=
C1s+1R12
−1R12
−1R12
C2s+1R12
+1R20
!
"
#####
$
%
&&&&&
Y (s)
T1T2
!
"##
$
%&&+
0
−1R20
!
"
###
$
%
&&&T0
Si se usa una analogía eléctrica donde las temperaturas equivalen a tensiones y las potencias térmicas equivalen a corrientes, la matriz Y(s) sería una matriz de admitancias operacionales. No obstante, no es necesario recurrir a esa analogía para obtener la ecuación matricial anterior y basta con plantear el balance de potencia térmica en cada medio.
Aplicando el principio de superposición y la regla de Cramer, se pueden calcular las dos funciones de transferencia deseadas:
T1
Pi
=
1 − 1R12
0 C2s+1
R12
+ 1R20
⎡
⎣
⎢⎢⎢⎢⎢
⎤
⎦
⎥⎥⎥⎥⎥
Y (s)=
R12 + R20( ) C2
R12R20
R12 + R20
s+1⎛
⎝⎜⎞
⎠⎟
C1C2R12R20s2 + R12C1 + R20C1 + R20C2( )s+1
T1
T0
=
0 − 1R12
1R20
C2s+1
R12
+ 1R20
⎡
⎣
⎢⎢⎢⎢⎢
⎤
⎦
⎥⎥⎥⎥⎥
Y (s)= 1
C1C2R12R20s2 + R12C1 + R20C1 + R20C2( )s+1
También es posible obtener estas funciones de transferencia a partir de un diagrama de bloques aplicando el álgebra de diagrama de bloques. En este caso, el diagrama tendrá dos entradas y una salida. Como ya se ha mencionado para otros tipos de sistemas, es ventajoso que el diagrama de bloques contenga únicamente ganancias, sumadores e integradores. De esta forma podremos simular la respuesta libre para unas determinadas
4–26
condiciones iniciales y también podremos acceder fácilmente no sólo a la salida sino a cualquier otra variable de interés en el sistema.
Para obtener el diagrama de bloques, se debe usar un integrador por cada medio presente en el sistema, excluyendo el medio exterior. Las salidas de estos integradores son las temperaturas de cada medio mientras que las entradas se corresponden con las derivadas temporales de esas temperaturas. Para completar el diagrama de bloques basta con despejar las derivadas de las temperaturas a partir de las ecuaciones de balance de potencia térmica en cada medio y construir dichas ecuaciones usando un sumador situado a la entrada de cada integrador. Finalmente, se debe localizar la variable de salida en el diagrama de bloques o, si no está presente, generarla mediante una ecuación adicional que la relacione con la temperatura de los medios.
Para el ejemplo 4.4, las ecuaciones que nos dan las derivadas temporales de las temperaturas para construir el diagrama de bloques son las siguientes:
1 1 2
1 12
1i
dT T TPdt C R
⎛ ⎞−= −⎜ ⎟⎝ ⎠
2 02 2 1
2 12 20
1 T TdT T Tdt C R R
⎛ ⎞−−= − −⎜ ⎟⎝ ⎠
Usando estas ecuaciones, resulta el diagrama de bloques mostrado en la figura 4.10.
dT1/dt T1 dT2/dt T2
1T1
1s
1s
1/R20
1/R12
1/R12 + 1/R20
1/R12
1/C21/R121/C1
2T0
1Pi
Figura 4.10. Diagrama de bloques del sistema térmico
En el caso de que la temperatura del medio exterior se considere constante durante el intervalo temporal en el cual interesa estudiar el sistema, es conveniente eliminar su influencia en las ecuaciones de cada medio. Para ello es necesario trabajar con temperaturas incrementales respecto a la temperatura exterior, teniendo en cuenta que las derivadas temporales de la temperatura absoluta y de la temperatura incremental coinciden si se supone constate la temperatura del medio exterior. De esta manera resultan las siguientes ecuaciones de balance de potencia térmica para cada medio:
4–27
1 1 21
12i
d T T TP Cdt RΔ Δ −Δ= +
2 2 1 22
12 20
0 d T T T TCdt R RΔ Δ −Δ Δ= + +
Siendo 1 1 0T T TΔ = − y 2 2 0T T TΔ = − . Si se aplica la transformada de Laplace y se organizan las ecuaciones de forma matricial, resulta:
Pi0
!
"##
$
%&&=
C1s+1R12
−1R12
−1R12
C2s+1R12
+1R20
!
"
#####
$
%
&&&&&
Y (s)
ΔT1ΔT2
!
"##
$
%&&
Se puede observar que en la ecuación anterior ha desaparecido la temperatura del medio exterior como se deseaba. A partir de aquí, el procedimiento para obtener la función de transferencia entre Pi e ΔT1 es idéntico al descrito previamente, ya sea usando la regla de Cramer o bien construyendo un diagrama de bloques y reduciéndolo posteriormente.
4.6 Sistemas de conducción de fluidos
Por último, en esta sección se presenta el modelado de sistemas de conducción de fluidos suponiendo comportamiento lineal e invariante en el tiempo. Se considera, por simplicidad, que el fluido se encuentra en estado líquido y nunca en estado gaseoso. Este tipo de sistemas está compuesto por depósitos que almacenan el fluido y tuberías que interconectan esos depósitos o bien vierten un caudal del fluido al exterior (desagüe libre). Además, existe habitualmente en el sistema un suministro externo de caudal mediante una bomba. Las variables que se manejan son los niveles en los depósitos y los caudales por las tuberías. Con el fin de simplificar el problema, se supondrá que todas las tuberías que interconectan depósitos están dispuestas horizontalmente, con el fin de ignorar la influencia del peso del fluido sobre el caudal.
A la hora de obtener el modelo o función de transferencia del sistema de conducción de fluidos, la entrada será habitualmente un caudal de fluido externo aportado al sistema mediante una bomba, mientras que la salida puede ser el nivel de un depósito o el caudal por una tubería. Para modelar este tipo de sistemas sólo se requiere plantear una ecuación de balance de volumen de fluido en cada depósito y aplicar la segunda ley de Newton a la masa de fluido que se desplaza por cada tubería.
• Balance de volumen de fluido en un depósito: En cualquiera de los depósitos presentes en el sistema, el volumen de fluido en su interior cambia cuando hay un caudal neto de entrada o salida al depósito.
4–28
Este caudal neto se calcula como la diferencia entre la suma de los caudales de entrada y la suma de los caudales de salida. Los caudales de entrada pueden provenir de una bomba que vierte su caudal sobre el depósito, de una tubería que conecta este depósito con otro, o bien de un desagüe libre en otro depósito que vierte sobre éste. Los caudales de salida se corresponden con los que se evacúan por tuberías que conectan este depósito con otros depósitos o bien por desagües libres en el depósito considerado. Suponiendo que el volumen de fluido en el depósito es V, que su nivel es h, que su sección es constante y vale A, que hay n caudales de entrada qij y m caudales de salida qoj, la ecuación de balance de volumen en el depósito sería:
1 1
n m
ij ojj j
dV dhA q qdt dt = =
= = −∑ ∑
• Equilibrio de fuerzas en una tubería: Supongamos la tubería horizontal que se muestra en la figura 4.11 que tiene una longitud L, una sección A y por la que circula una masa de fluido con velocidad v y caudal q = Av. Además se supone que existen presiones distintas de valores p1 y p2 a ambos lados de la tubería, determinadas por dos depósitos de secciones A1 y A2 y niveles h1 y h2, respectivamente. Se desea relacionar el caudal q que circula por la tubería con los niveles h1 y h2 de los depósitos.
Figura 4.11. Tubería conectada por dos depósitos
En primer lugar, es necesario relacionar las presiones p1 y p2 con los niveles h1 y h2. Para ello recurrimos al equilibrio de fuerzas sobre la masa de fluido contenida en cada depósito. Esa masa de fluido se ve sometida a tres fuerzas: la fuerza que ejerce la presión en el fondo del depósito, el peso de la masa de fluido en el depósito y la fuerza ejercida en la parte superior por la presión atmosférica p0.
1 1 1 1 0 1p A Ah g p Aρ= +
2 2 2 2 0 2p A A h g p Aρ= +
Siendo ρ la densidad del fluido y g la gravedad. Si se despejan las presiones en función de los niveles, se puede comprobar que las secciones de los depósitos no influyen en estas relaciones.
h1 h2
p1 p2 q
L
A
A1 A2
4–29
1 1 0p h g pρ= +
2 2 0p h g pρ= +
Nótese que si en uno de los lados de la tubería se dispone de un desagüe libre, se puede considerar que la presión en ese extremo será la presión atmosférica p0, y por lo tanto, el desagüe libre equivale a un depósito con nivel h = 0.
A continuación, aplicamos la 2ª ley de Newton a la masa de fluido contenida en la tubería. Esta masa se ve sometida en la dirección del movimiento a las fuerzas provocadas por las presiones a ambos lados de la tubería, que son de sentido contrario, y a una fuerza de rozamiento FR con las paredes de la tubería que se opone al movimiento.
( )1 2 1 2R Rdv dqAL L p A p A F A g h h Fdt dt
ρ ρ ρ= = − − = − −
Despejando la derivada temporal del caudal por la tubería, resulta:
( )1 2RFdq Ag h h
dt L Lρ= − −
Los ensayos experimentales demuestran que la fuerza de fricción es
proporcional a qα, con α entre 1.75 y 2, dependiendo del tipo de fluido y de si el régimen del caudal es turbulento o laminar, lo cual introduce un término no lineal en esta ecuación. Para poder aplicar todas las técnicas estudiadas hasta ahora para la obtención de funciones de transferencia, se supondrá una relación lineal entre la fuerza de fricción y el caudal, es decir una fricción de tipo viscoso con constante Kf. Habitualmente, esta aproximación lineal se aplica alrededor de un punto de operación del sistema, de tal manera que las variables que se manejan en la ecuaciones pasan a ser incrementales con respecto a sus valores en el punto de operación. Aunque esta simplificación provoca una pérdida de precisión, tanto mayor cuanto más nos alejamos del punto de operación, ofrece como contrapartida la potencia de cálculo y análisis de la transformada de Laplace. Usando esta simplificación, resulta:
dqdt=AgL
h1 − h2( )−K f qρL
LAg
dqdt+K f
AgL
R
q = LAg
dqdt+ Rq = h1 − h2
Donde todas las variables pasan a ser incrementales con respecto a sus valores en el punto de operación considerado, aunque no se ha
4–30
modificado la notación en las variables por simplicidad. A la constante R se la denomina resistencia hidráulica de la tubería y es el parámetro que se utilizará para caracterizar de forma aproximada la pérdida de presión en la tubería provocada por la fricción. En el caso de tuberías cortas con variaciones lentas de caudal, se puede eliminar en la ecuación anterior el término correspondiente a la derivada temporal del caudal, resultando:
1 2h hqR−=
Y para el caso de un desagüe libre en la base de un depósito con nivel h, queda:
hqR
=
La ecuación correspondiente a un desagüe libre suele deducirse habitualmente a partir del proceso de conversión entre energía potencial y energía cinética que se produce en el fluido evacuado a través del desagüe libre, ya que no existe pérdida de energía por fricción. En este caso se puede plantear:
mgh = 12mv2
q = av = a 2gC
h =C h
donde m es la masa de fluido en el depósito, h es el nivel del depósito, v es la velocidad de escape del fluido por el desagüe libre, a la sección del desagüe y q el caudal correspondiente. Si se define un punto de operación con nivel h0 en el depósito y se trabaja con variables incrementales alrededor de este punto de operación, resulta:
Δq = C2 h0
∂q∂h#
$%h=ho
Δh = ΔhR
Siendo R la resistencia hidráulica del desagüe. Esta ecuación coincide con la deducida a partir de la ecuación de la tubería si se prescinde por simplicidad de la notación incremental.
Ejemplo 4.5. Considérese el sistema de conducción de fluidos de la figura 4.12. Se trata de un sistema que consta de dos depósitos de secciones A1 y A2 y niveles h1 y h2, respectivamente, con respecto a un punto de operación conocido. Los depósitos están interconectados mediante una tubería de longitud L, sección A, caudal q12 y resistencia hidráulica R12, y con un
4–31
desagüe libre en el segundo depósito con resistencia hidráulica R20 y por el que se vierte al exterior un caudal q20. Sobre el primer depósito se vierte mediante una bomba un caudal qi que se considerará como variable de entrada al sistema. El objetivo será obtener la función de transferencia entre el caudal qi (entrada) y el nivel h2 en el segundo depósito considerando la dinámica de la tubería o despreciándola (tubería de corta longitud). Se supone que todas las variables son incrementales con respecto a un punto de operación conocido.
Figura 4.12. Sistema de conducción de fluidos
En primer lugar, se obtendrá la función de transferencia entre qi y h2 teniendo en cuenta la dinámica de la tubería. Las ecuaciones correspondientes al balance de volumen de fluido en los depósitos 1 y 2 y la ecuación de la tubería para el sistema del ejemplo 4.5 son las siguientes:
11 12idhA q qdt
= −
2 22 12 20 12
20
dh hA q q qdt R
= − = −
1212 12 1 2
dqL R q h hAg dt
+ = −
A continuación, se aplica la transformada de Laplace a todas las ecuaciones y se organizan en forma de ecuación matricial:
Qi
0
!
"##
$
%&&=
A1s+1
LAg
s+ R12−
1LAg
s+ R12
−1
LAg
s+ R12A2s+
1R20
+1
LAg
s+ R12
!
"
#######
$
%
&&&&&&&
Y (s)
H1
H2
!
"##
$
%&&
L, A, R12
A1 A2
R20
h1 h2
qi
q12
q20
1 2
4–32
Si se usa una analogía eléctrica donde los caudales equivalen a corrientes y los niveles a tensiones, la matriz Y(s) sería una matriz de admitancias operacionales. No obstante, no es necesario recurrir a esa analogía para obtener la ecuación matricial anterior y basta con plantear el balance de volumen de fluido en cada depósito.
Aplicando superposición y la regla de Cramer, se puede calcular la función de transferencia deseada:
1
12
2112 1 12
2
3 21 2 121 2 12 1 2
20 20 20
1 1
1 01
( ) 11i
A s L s RAg
L A Ls R s A R sAgH Ag
Q Y s A A L RLs A A R s A A sAg AgR R R
⎡ ⎤+⎢ ⎥+⎢ ⎥
⎢ ⎥⎢ ⎥
−⎢ ⎥⎢ ⎥+ + +⎢ ⎥⎣ ⎦= =
⎛ ⎞⎛ ⎞ ⎛ ⎞+ + + + + +⎜ ⎟⎜ ⎟ ⎜ ⎟⎜ ⎟⎝ ⎠ ⎝ ⎠⎝ ⎠
También es posible obtener esta función de transferencia a partir de un diagrama de bloques aplicando el álgebra de diagrama de bloques. Para obtener el diagrama de bloques, se debe usar un integrador por cada depósito y cada tubería en la que se modele su dinámica. Las salidas de estos integradores son los niveles de cada depósito y el caudal de cada tubería, mientras que las entradas se corresponden con las derivadas temporales de esas variables. Para completar el diagrama de bloques basta con despejar las derivadas de los niveles y caudales a partir de las ecuaciones del sistema y construir dichas ecuaciones usando un sumador situado a la entrada de cada integrador. Finalmente, se debe localizar la variable de salida en el diagrama de bloques o, si no está presente, generarla mediante una ecuación adicional que la relacione con las variables que sí aparecen en el diagrama.
Para el ejemplo 4.5, las ecuaciones que nos dan las derivadas temporales de los niveles de los depósitos 1 y 2 y de la tubería para construir el diagrama de bloques son las siguientes:
( )112
1
1i
dh q qdt A
= −
2 212
2 20
1dh hqdt A R
⎛ ⎞= −⎜ ⎟
⎝ ⎠
( )121 2 12 12
dq Ag h h R qdt L
= − −
Usando estas ecuaciones, resulta el diagrama de bloques mostrado en la figura 4.13.
4–33
dh1/dt h1 dq12/dt q12h2dh2/dt
1h2
1s
1s
1s
R12
1/R20
Ag/L 1/A21/A11qi
Figura 4.13. Diagrama de bloques del sistema de conducción de fluidos suponiendo dinámica en la tubería
Finalmente, se obtendrá la función de transferencia entre qi y h2 despreciando la dinámica de la tubería. Las ecuaciones correspondientes al balance de volumen de fluido en los depósitos 1 y 2 y la ecuación de la tubería para este caso son las siguientes:
1 1 21 12
12i i
dh h hA q q qdt R
−= − = −
2 22 12 20 12
20
dh hA q q qdt R
= − = −
A continuación, se aplica la transformada de Laplace a todas las ecuaciones y se organizan en forma de ecuación matricial:
Qi
0
!
"##
$
%&&=
A1s+1R12
−1R12
−1R12
A2s+1R20
+1R12
!
"
#####
$
%
&&&&&
Y (s)
H1
H2
!
"##
$
%&&
Aplicando superposición y la regla de Cramer, se calcula la función de transferencia deseada:
( )( )
112
20 1 121222
1 2 12 20 1 20 1 12 2 20
1 1
1 01
( ) 1i
A sR
R AR sRHQ Y s A A R R s AR AR A R s
⎡ ⎤+⎢ ⎥⎢ ⎥⎢ ⎥−⎢ ⎥ +⎣ ⎦= =
+ + + +
También es posible obtener esta función de transferencia a partir de un diagrama de bloques aplicando el álgebra de diagrama de bloques. Para obtener el diagrama de bloques, se debe usar un integrador por cada depósito. Las salidas de estos integradores son los niveles de cada depósito, mientras que las entradas se corresponden con las derivadas temporales de los niveles. Para completar el diagrama de bloques basta con despejar las derivadas de los niveles de las ecuaciones del sistema y construir dichas ecuaciones usando un
4–34
sumador situado a la entrada de cada integrador. Finalmente, se debe localizar la variable de salida en el diagrama de bloques o, si no está presente, generarla mediante una ecuación adicional que la relacione con los niveles de los depósitos.
Las ecuaciones que nos dan las derivadas temporales de los niveles de los depósitos 1 y 2 para construir el diagrama de bloques son las siguientes:
1 1 2
1 12
1i
dh h hqdt A R
⎛ ⎞−= −⎜ ⎟⎝ ⎠
2 212
2 20
1dh hqdt A R
⎛ ⎞= −⎜ ⎟
⎝ ⎠
Usando estas ecuaciones, resulta el diagrama de bloques mostrado en la figura 4.14.
dh1/dt h1 h2dh2/dt
1h2
1s
1s
1/R12
1/R121/R20 + 1/R12
1/R12 1/A21/A11qi
Figura 4.14. Diagrama de bloques del sistema de conducción de fluidos despreciando la dinámica en la tubería
Nótese que, al haber utilizado variables incrementales en todo el análisis anterior, para obtener el valor absoluto de cada variable habría que añadirle su valor en en el punto de operación considerado.